Floyd算法详解：实现思路与优化技巧

"Floyd算法是一种用于寻找图中所有节点间最短路径的算法，具有O(n^3)的时间复杂度。该算法通过迭代的方式检查所有可能的中间节点，以更新最短路径信息。" Floyd-Warshall算法，通常简称为Floyd算法，是一个解决全连接图中两两节点间最短路径问题的有效方法。它基于动态规划的思想，通过逐步考虑所有可能的中间节点来更新最短路径。算法的核心在于三重循环，依次遍历所有节点，以检查是否存在更短的路径。 1. **算法步骤**: - 初始化：首先，根据图的边权重初始化一个二维距离矩阵Dis，其中Dis[i][j]表示节点i到节点j的初始距离。对于有向图，如果节点i不能直接到达节点j，则Dis[i][j]设置为无穷大，表示无法到达；对于无向图，Dis[i][j]等于直接连接i和j的边的权重，如果不存在直接连接，则设为无穷大。 - 迭代：使用三层循环，分别遍历节点i、k和j。外层循环k遍历所有节点，内层两个循环i和j也遍历所有节点。 - 检查路径：在每次迭代中，算法检查是否存在通过中间节点k的更短路径。如果Dis[i][k]加上Dis[k][j]小于当前Dis[i][j]，则更新Dis[i][j]为Dis[i][k] + Dis[k][j]，表示找到了新的最短路径。 - 结束条件：当所有可能的中间节点k都被检查过，Dis矩阵中的每个元素都包含了对应节点对之间的最短路径。 2. **循环顺序的重要性**: - 正确的循环顺序是先k后i再j，即外层循环k，然后是i，最后是j。如果反过来，可能会导致算法在早期就错误地确定了某些路径的最短距离，因为没有机会检查后续可能出现的更短路径。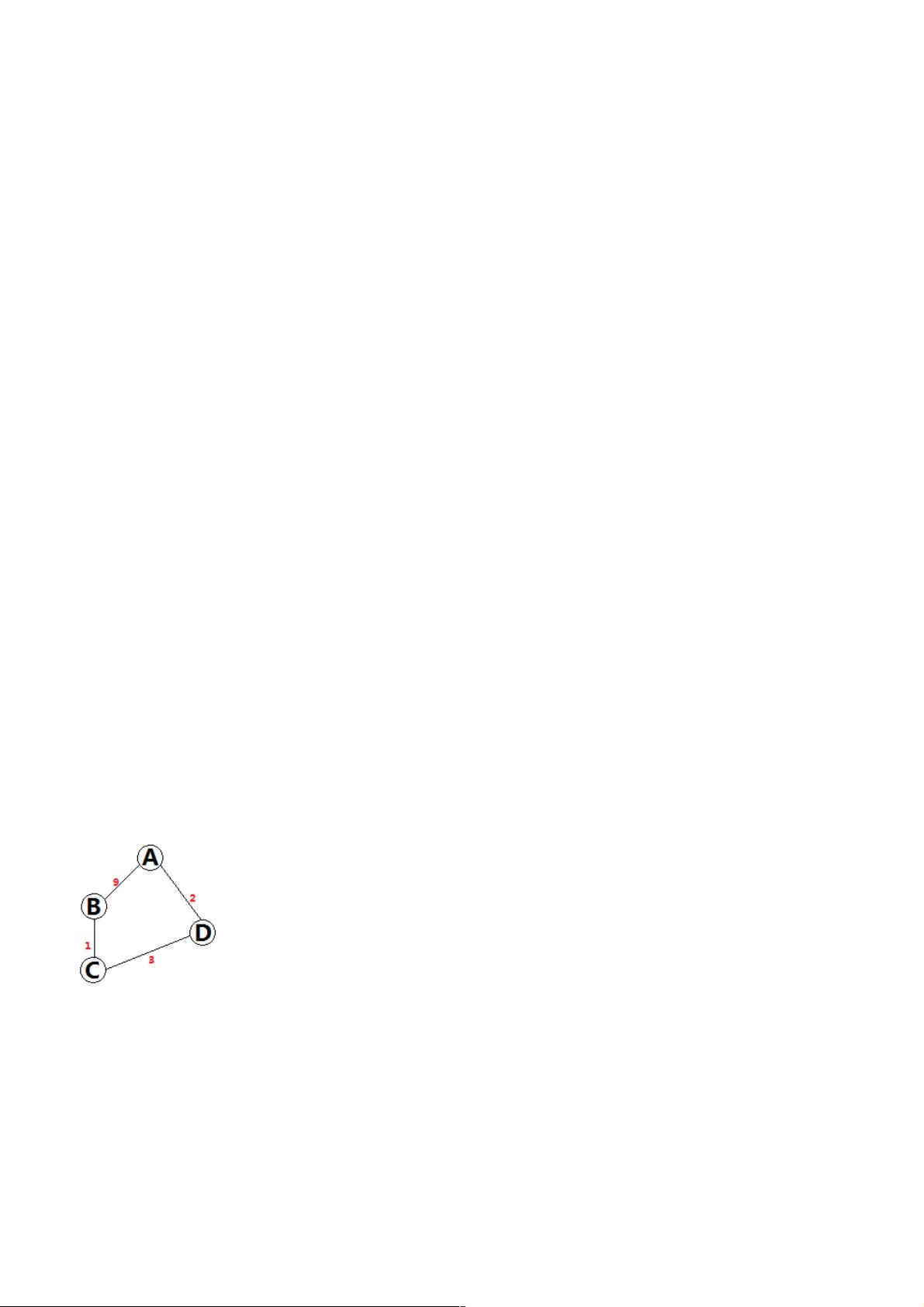 - 举例说明，如描述中的例子，图中节点A到节点B的最短路径是A->D->C->B，如果按照i、j、k的顺序进行检查，算法将过早地认为A到B的最短路径是A->B，而忽略了通过其他节点的可能路径。 3. **适用场景**: - Floyd算法适用于求解具有大量边和节点的图的最短路径问题，尤其在图中可能存在负权边但没有负权环的情况下。对于不含负权边的图，Dijkstra算法可能是更好的选择，因为它运行更快，但对于含有负权边的图，Floyd算法能正确处理。 4. **优化与限制**: - 虽然Floyd算法的时间复杂度是O(n^3)，但因为其简单性和通用性，在许多实际应用中仍然被广泛使用。对于大型图，可以采用并行化或分布式计算来提高效率。 - 由于算法涉及到全部节点的遍历，对于稀疏图（边的数量远小于节点数量的平方）来说，Floyd算法可能不如其他算法（如Johnson算法）高效，因为这些算法通常能利用图的稀疏性减少计算量。 5. **实例代码**: 实现Floyd算法的代码通常包含三个嵌套循环，以确保所有节点组合都被检查。在上述代码示例中，外层循环k遍历所有节点，然后i和j分别再次遍历所有节点，以检查通过k节点的最短路径。 通过理解和掌握Floyd算法，我们可以有效地解决图论问题中的最短路径问题，为网络路由、物流调度、社会网络分析等领域提供有力的工具。