7
Consider a simple model of a resource-exporting country that has an endowment of units of natural
resources, which it exports in exchange for consumption goods. Advanced economies import the natural
resources and combine them with skilled labor to produce consumption goods according to the Cobb-
Douglas production function
=
(
,
)
=
where Y is world output. In competitive markets, this production function results in factor shares for
skilled labor and 1 for natural resources.
4
One interpretation of the described production function – in
the spirit of Zeira (1998) and Acemoglu and Autor (2011) – is that final goods are produced using a series
of tasks that are combined in Cobb-Douglas fashion, where a fraction of the tasks employ skilled labor
and the remaining fraction 1 relies on natural resources.
In our simple model, the factor share 1 of natural resources is also the income share of the resource-
exporting country in world output. If we use the price of final output as the numeraire, then the marginal
product of natural resources
=
(
1
)
/ simultaneously represents the terms-of-trade (i.e. the
price of export goods over the price of import goods) of the resource-exporting country.
Now consider a technological innovation that allows producers to economize on the use of natural
resources and instead rely more on skilled labor, resulting in a change to the Cobb-Douglas coefficient in
our production function of > 0. In the task-based interpretation of our framework, we could view this as
a fraction of the tasks relying on natural resources being replaced by skilled labor. Producers have a
choice between the old and the new technology so = max
{
(
,
)
, (, )
}
where we denote the new
production function with a prime. They find it optimal to deploy the new technology when natural
resources are sufficiently scarce, as captured by the following lemma:
Lemma (Use of Natural Resource-Saving Innovation): Producers will find it optimal to use the new
technology described by > 0 if natural resources are sufficiently scarce, i.e. if the world economy’s
natural-resource/skilled-labor ratio is below a threshold,
<
Given the units in which the inputs in the production function above are denoted, the threshold is = 1 in
our example.
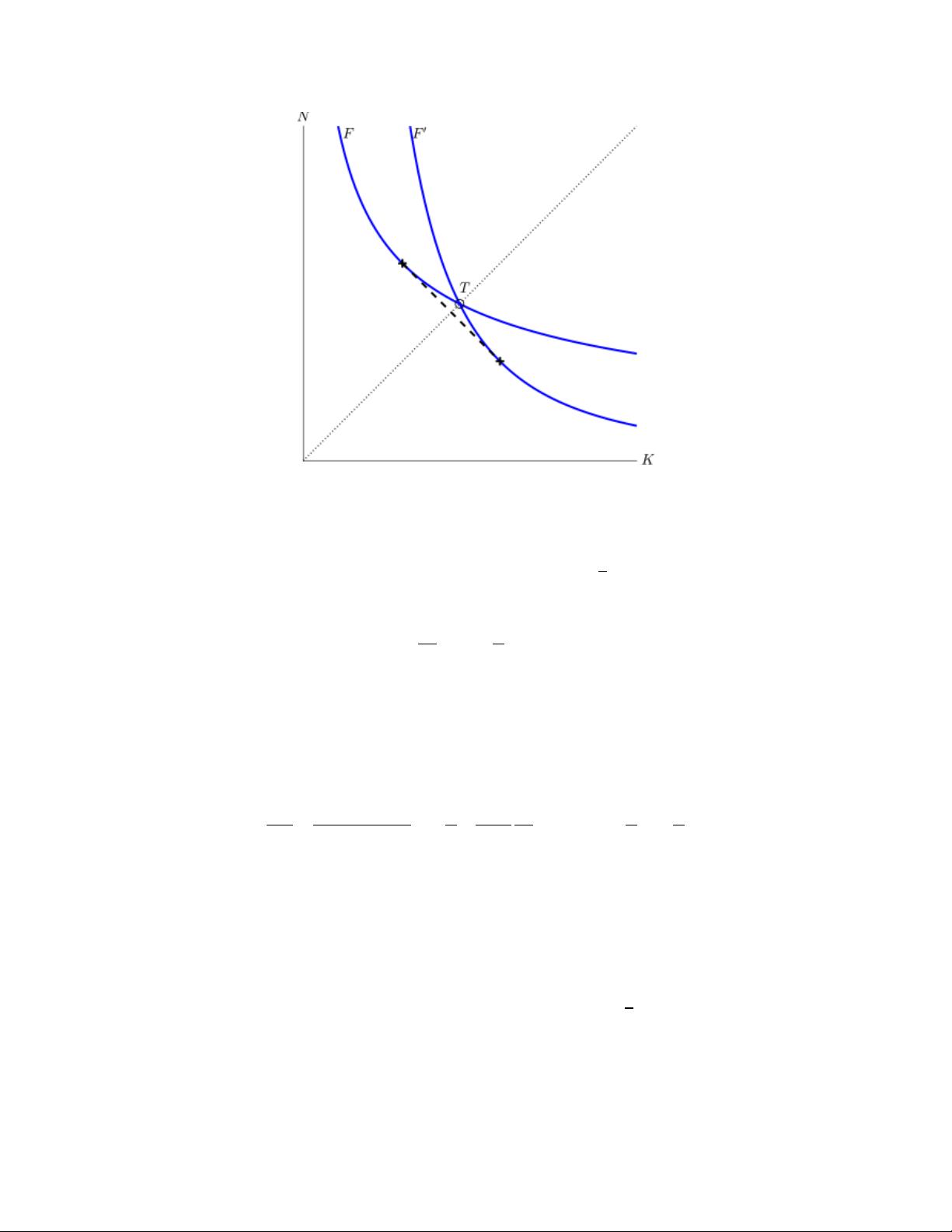
Figure 2 illustrates the isoquants of the old and new technology and for a discrete change > 0.
The two isoquants intersect at a threshold point , which corresponds to the natural resource/labor ratio
at which a producer finds it optimal to switch technology. The dotted ray from the origin through point
separates the factor space into two areas: if the natural resource intensity of the world economy is greater
than the threshold (corresponding to the area above the ray), the old production technology is more
efficient – the corresponding isoquant reflects that within this area, the old technology requires fewer
inputs. If the resource intensity is below the threshold, the new technology is more efficient and requires
fewer inputs to produce a given amount of output. The economy’s overall production possibilities are
given by the envelope, i.e. the convex hull, of the two isoquants, indicated by a dashed line, since it is
optimal for producers to use a mix of the two technologies over the indicated segment. That means that
4
It is straightforward to expand the model to capture imperfect competition.