四元数与三维旋转：直观解析

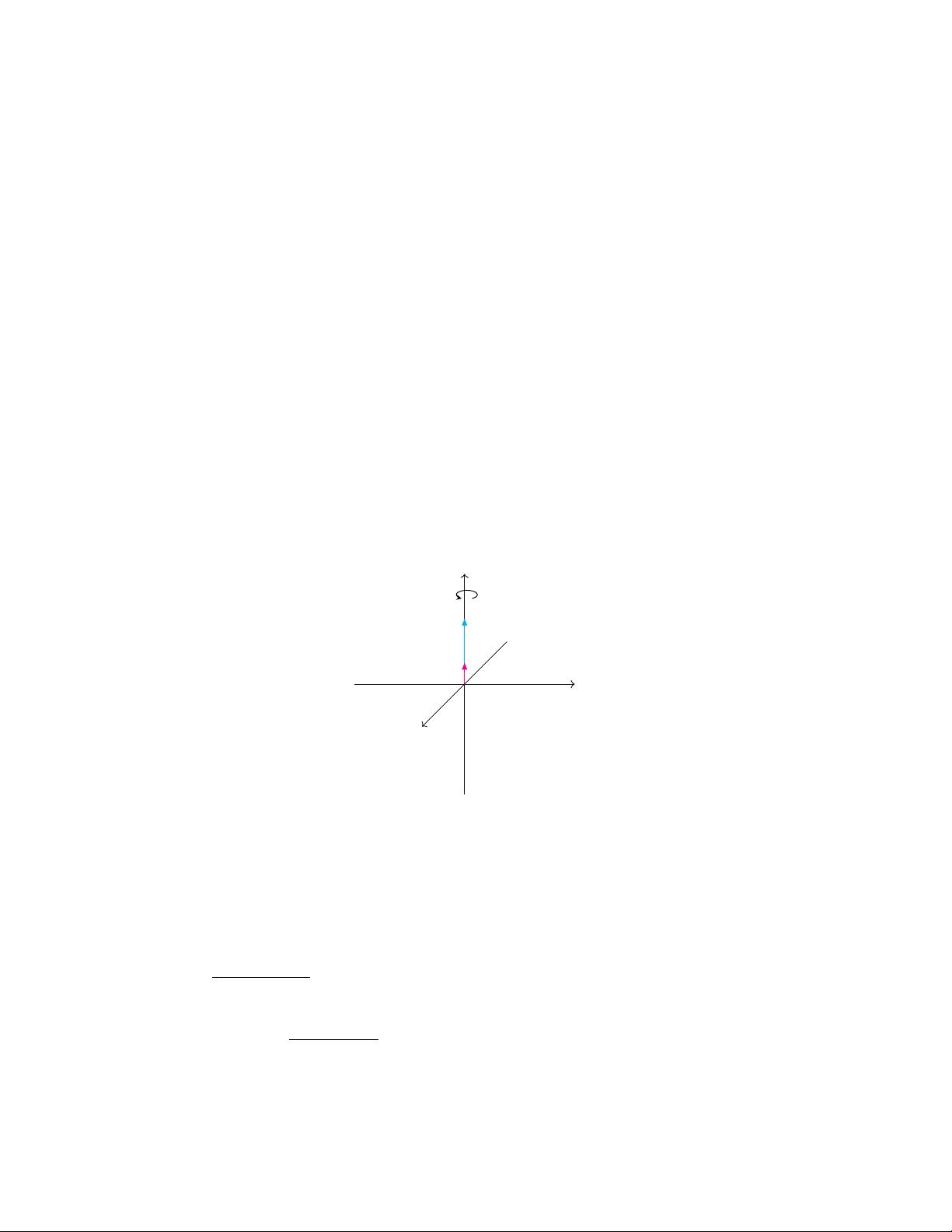
该资源是一篇关于四元数与三维旋转关系的文章，作者发现现有的资料在解释四元数时较为抽象或不清晰，因此决定用自己的方式来阐述这一主题。文章主要利用几何学和线性代数的基础知识来解析四元数与三维旋转的联系，适合对计算机图形学感兴趣的读者。作者提供了MATLAB/Octave的示例代码和相关动画，并在GitHub上分享。文章末尾提到了复数作为引入四元数的预备知识。 详细知识点: 1. **四元数与三维旋转**: 四元数是一种扩展复数的概念，用于表示三维空间中的旋转。复数仅能处理二维旋转，而四元数可以方便地描述三维空间中的旋转操作，避免了万向节死锁问题，常用于3D图形学和机器人学。 2. **复数基础**: 复数由实部和虚部构成，形式为`z = a + bi`，其中`a`是实部，`b`是虚部，`i`是虚数单位，满足`i^2 = -1`。复数的乘法遵循特定规则，可以形成复数平面，通过极坐标表示可以关联到2D旋转。 3. **从复数到四元数**: 四元数同样基于线性组合，但使用四个分量，形式为`q = w + xi + yj + zk`，其中`w, x, y, z`都是实数，`i, j, k`是相互正交的虚数单位，满足`ij=k, jk=i, ki=j`和它们各自的平方等于-1。四元数的乘法规则更加复杂，但保持了乘法的结合律和分配律。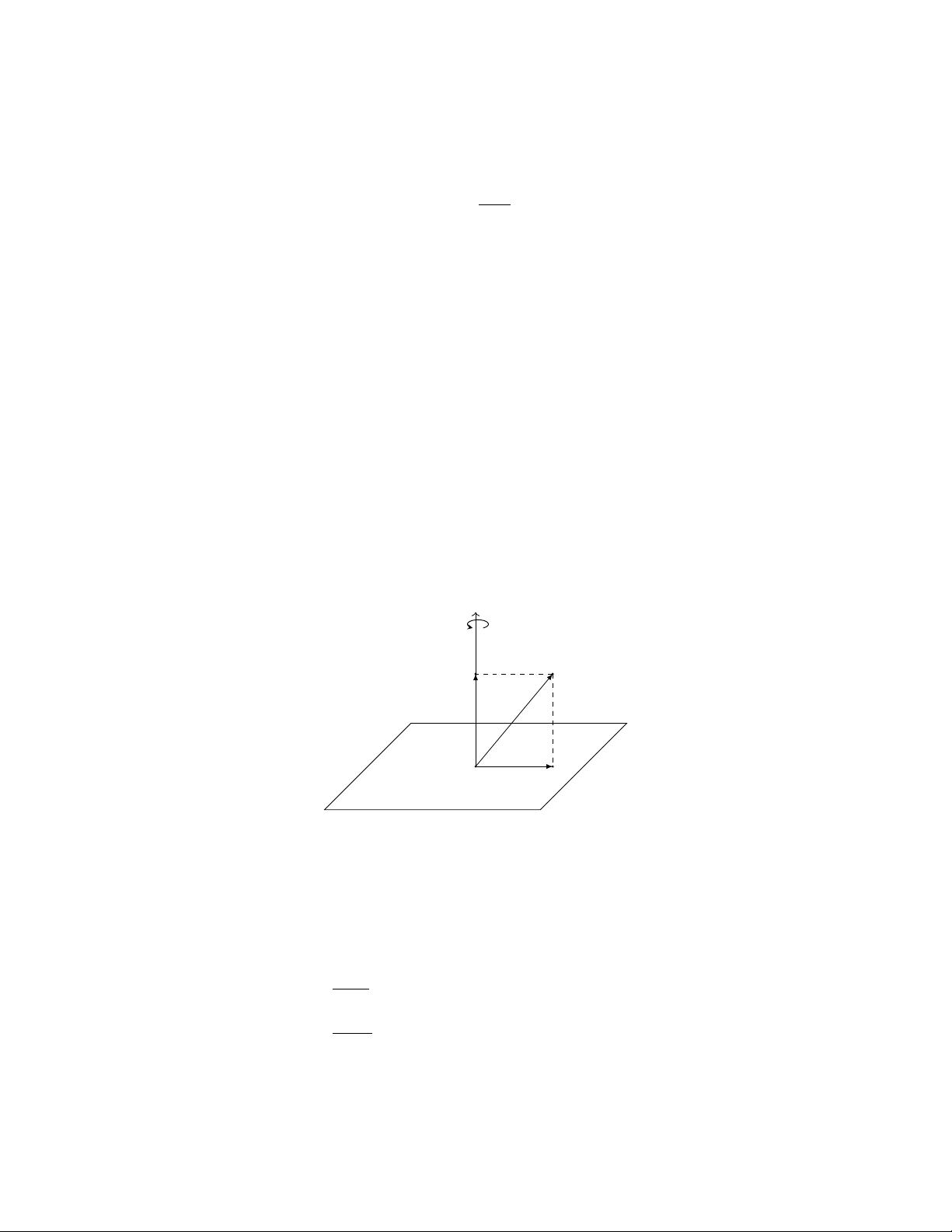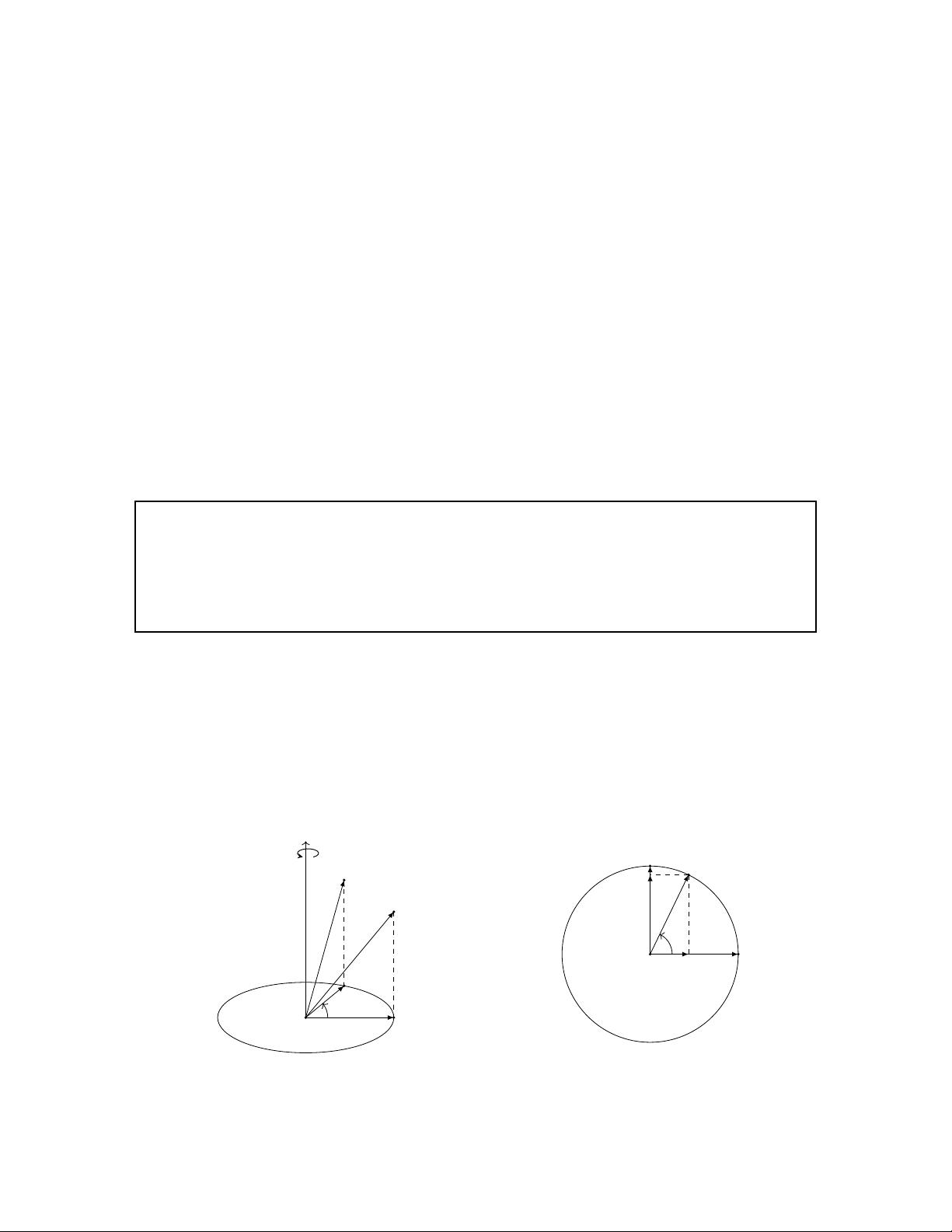 4. **三维旋转与四元数的关系**: 通过四元数可以简洁地表达旋转轴和旋转角度。单位四元数（模长为1的四元数）与旋转矩阵等价，其中实部`w`对应于旋转轴的方向，虚部`(x, y, z)`对应于旋转轴上的向量部分，其长度表示旋转角度的一半。 5. **四元数运算及应用**: 四元数乘法可以表示两个旋转的组合，这在处理连续旋转时非常有用。在计算机图形学中，四元数用于存储和应用对象的旋转状态，简化了旋转的叠加和插值。 6. **四元数的几何直观**: 通过四元数的欧拉分解，可以直观地理解它是如何表示三维空间中的旋转。例如，通过旋转轴和旋转角度可以构造对应的四元数，反之亦然。 7. **矩阵变换与四元数**: 三维旋转可以用旋转矩阵表示，但矩阵运算有时会导致计算复杂性和内存消耗增加。四元数提供了更高效的存储和计算方式，特别是在处理大量旋转时。 8. **四元数的推广和拓展**: 文章可能还涉及四元数在更抽象的数学领域，如代数和物理中的应用，但这不是文章的重点。 9. **代码示例和交互性**: 作者提供的MATLAB/Octave代码和GIF动画有助于读者直观地理解四元数与旋转之间的关系，提供了一种实践性的学习方法。 10. **许可证信息**: 文章遵循了'CC BY-NC-SA 4.0'协议，要求在分享时署名、保持相同协议并禁止商业用途。 通过这些知识点，读者可以更好地理解和应用四元数，特别是在三维空间中的旋转表示和计算中。