归并排序详解：递归与非递归实现及复杂度分析

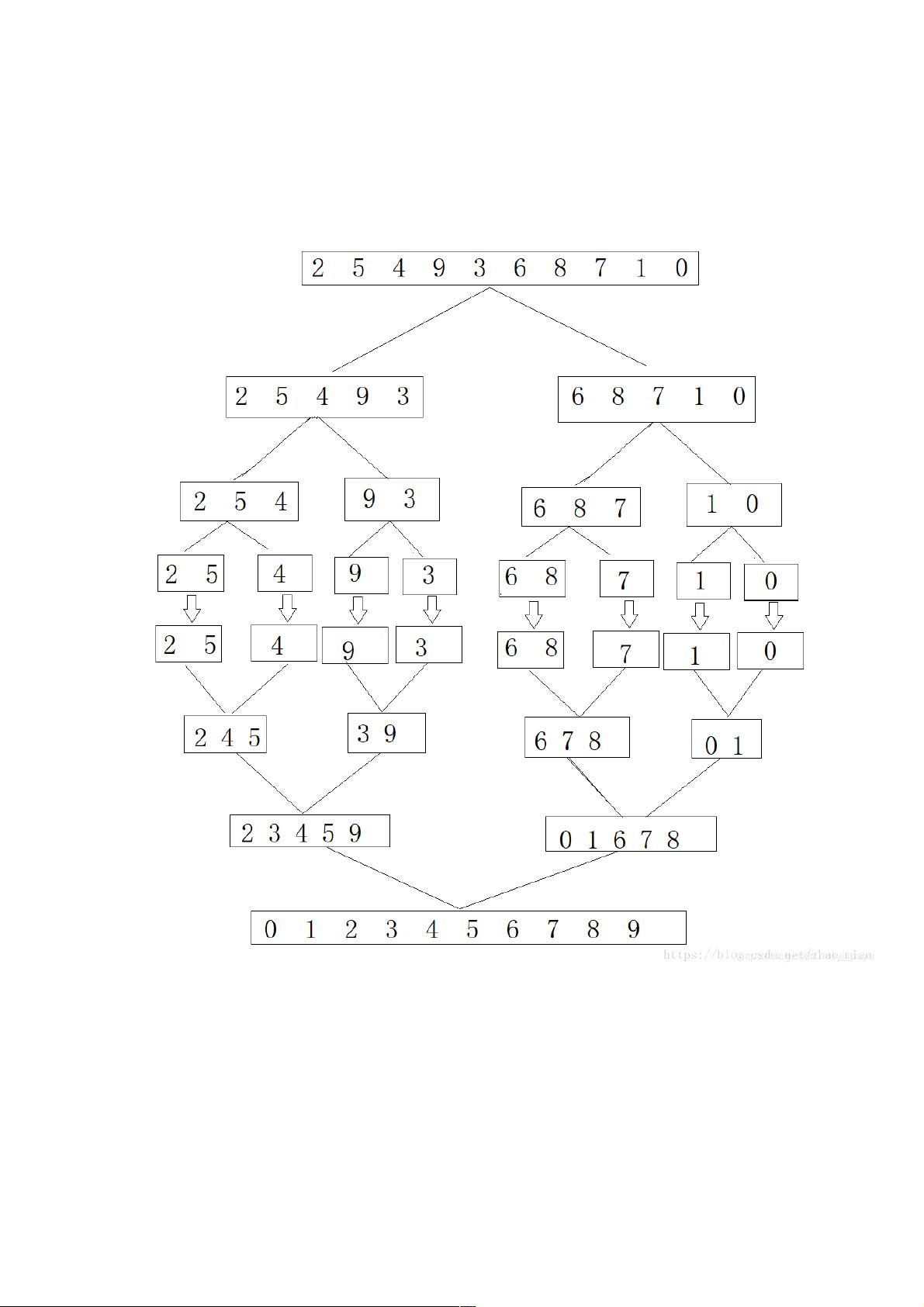
"本文主要介绍了归并排序的原理、递归和非递归实现方法以及算法复杂度分析。归并排序是一种基于分治策略的排序算法，与快速排序类似，但区别在于归并排序的划分基准是数组的中间元素。文章提供了一个递归版本的归并排序实现，并探讨了如何通过非递归方式优化。此外，还分析了归并排序的性能特点，包括时间复杂度和空间复杂度。" 1. 基本思想 归并排序的核心理念是分治法，即将大问题分解为小问题来解决。在排序过程中，首先将待排序的数组分成两个相等（或接近相等）的部分，然后分别对这两部分进行排序，最后将两个有序的部分合并成一个大的有序序列。这个过程类似于二分查找，但排序需要额外的合并步骤。 2. 代码实现 2.1 递归实现 归并排序的递归实现通常从一个包含所有元素的区间开始，递归地将区间一分为二，直到每个区间只包含一个元素（此时视为有序）。然后通过合并操作将这些有序区间合并回原数组，形成最终的有序序列。 2.2 优化—非递归实现 非递归实现归并排序通常使用循环结构，通过维护一个栈来保存待合并的区间。在初始化时，将整个数组作为一个区间压入栈中。每次从栈中弹出一个区间，将其一分为二，然后将这两个子区间重新压入栈中。重复此过程，直到栈为空，表示所有元素都已被排序。 3. 性能分析 归并排序的时间复杂度为O(n log n)，其中n是待排序元素的数量。这是因为每次划分操作将问题规模减半，而合并操作需要线性时间。空间复杂度为O(n)，因为需要额外的空间来存储合并过程中的临时数组。 归并排序的稳定性和分治策略使其在处理大数据量时表现出良好的性能，但其需要额外的存储空间，这可能成为其在内存有限情况下的局限。相比之下，快速排序在平均情况下也具有O(n log n)的时间复杂度，但在最坏情况下可能退化为O(n^2)，且不需要额外空间，因此在实际应用中两者各有优势，根据具体情况选择合适的排序算法。 总结，归并排序是一种高效的排序算法，尤其适用于大数据量和稳定性要求高的场景。通过理解其分治策略和实现细节，可以帮助我们更好地设计和优化算法，提高程序的效率。