Chapter 4 covers the innovation that made the most profound impact on the field of digital signal
processing, the fast Fourier transform (FFT). There we show the relationship of the popular radix 2
FFT to the DFT, quantify the powerful processing advantages gained by using the FFT, demonstrate
why the FFT functions as it does, and present various FFT implementation structures. Chapter 4 also
includes a list of recommendations to help the reader use the FFT in practice.
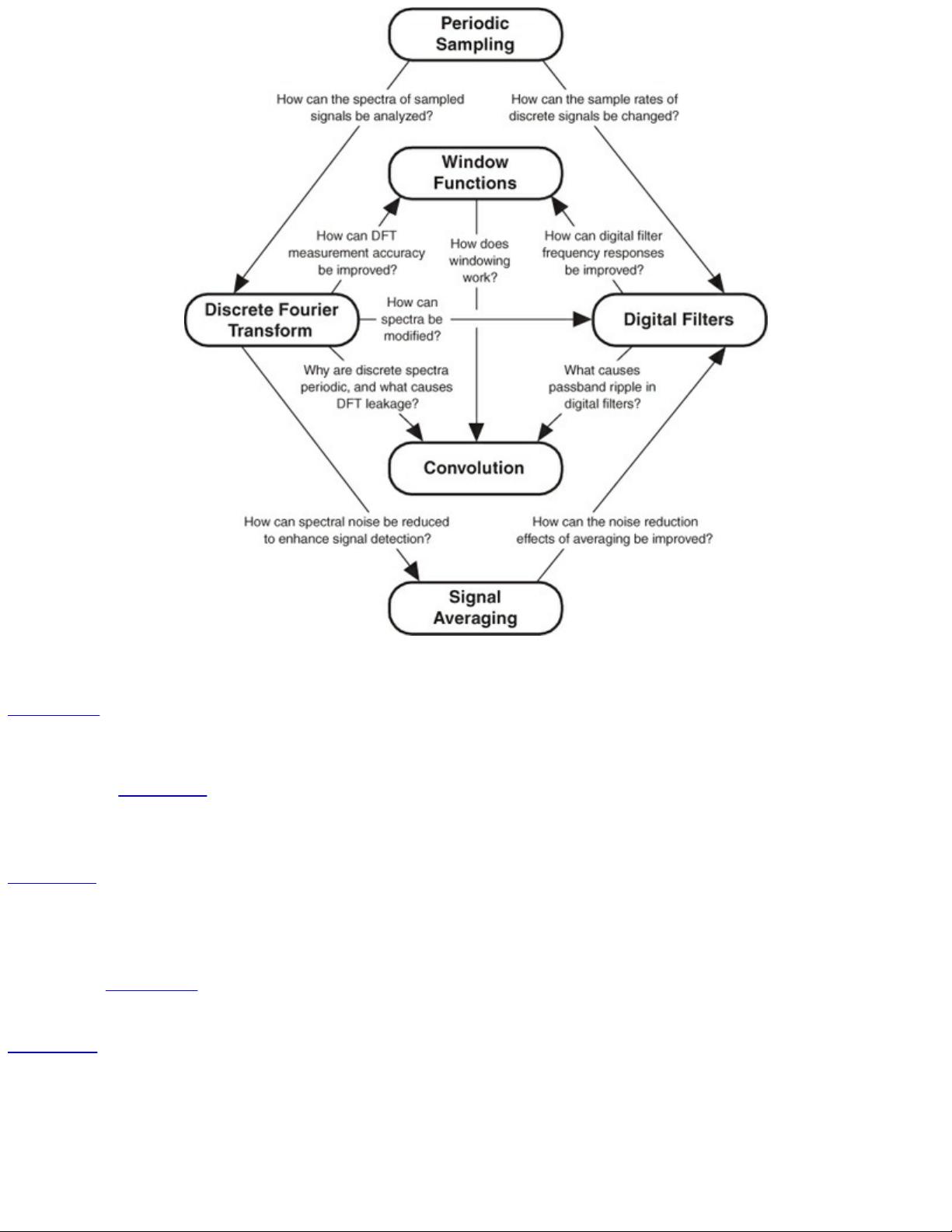
Chapter 5 ushers in the subject of digital filtering. Beginning with a simple lowpass finite impulse
response (FIR) filter example, we carefully progress through the analysis of that filter’s frequency-
domain magnitude and phase response. Next, we learn how window functions affect, and can be used
to design, FIR filters. The methods for converting lowpass FIR filter designs to bandpass and
highpass digital filters are presented, and the popular Parks-McClellan (Remez) Exchange FIR filter
design technique is introduced and illustrated by example. In that chapter we acquaint the reader with,
and take the mystery out of, the process called convolution. Proceeding through several simple
convolution examples, we conclude Chapter 5 with a discussion of the powerful convolution theorem
and show why it’s so useful as a qualitative tool in understanding digital signal processing.
Chapter 6 is devoted to a second class of digital filters, infinite impulse response (IIR) filters. In
discussing several methods for the design of IIR filters, the reader is introduced to the powerful
digital signal processing analysis tool called the z-transform. Because the z-transform is so closely
related to the continuous Laplace transform, Chapter 6 starts by gently guiding the reader from the
origin, through the properties, and on to the utility of the Laplace transform in preparation for learning
the z-transform. We’ll see how IIR filters are designed and implemented, and why their performance
is so different from that of FIR filters. To indicate under what conditions these filters should be used,
the chapter concludes with a qualitative comparison of the key properties of FIR and IIR filters.
Chapter 7 introduces specialized networks known as digital differentiators, integrators, and
matched filters. In addition, this chapter covers two specialized digital filter types that have not
received their deserved exposure in traditional DSP textbooks. Called interpolated FIR and
frequency sampling filters, providing improved lowpass filtering computational efficiency, they
belong in our arsenal of filter design techniques. Although these are FIR filters, their introduction is
delayed to this chapter because familiarity with the z-transform (in Chapter 6) makes the properties of
these filters easier to understand.
Chapter 8 presents a detailed description of quadrature signals (also called complex signals).
Because quadrature signal theory has become so important in recent years, in both signal analysis and
digital communications implementations, it deserves its own chapter. Using three-dimensional
illustrations, this chapter gives solid physical meaning to the mathematical notation, processing
advantages, and use of quadrature signals. Special emphasis is given to quadrature sampling (also
called complex down-conversion).
Chapter 9 provides a mathematically gentle, but technically thorough, description of the Hilbert
transform—a process used to generate a quadrature (complex) signal from a real signal. In this
chapter we describe the properties, behavior, and design of practical Hilbert transformers.
Chapter 10 presents an introduction to the fascinating and useful process of sample rate conversion
(changing the effective sample rate of discrete data sequences through decimation or interpolation).
Sample rate conversion—so useful in improving the performance and reducing the computational
complexity of many signal processing operations—is essentially an exercise in lowpass filter design.
As such, polyphase and cascaded integrator-comb filters are described in detail in this chapter.