Python概率分布与可视化全解析
3 浏览量
更新于2024-07-15
2
收藏 3.42MB PDF 举报
本文档是一篇全面介绍Python中各种概率分布及其可视化的教程,涵盖了连续型和离散型随机变量的众多分布,包括但不限于:
1. **术语与概念**:
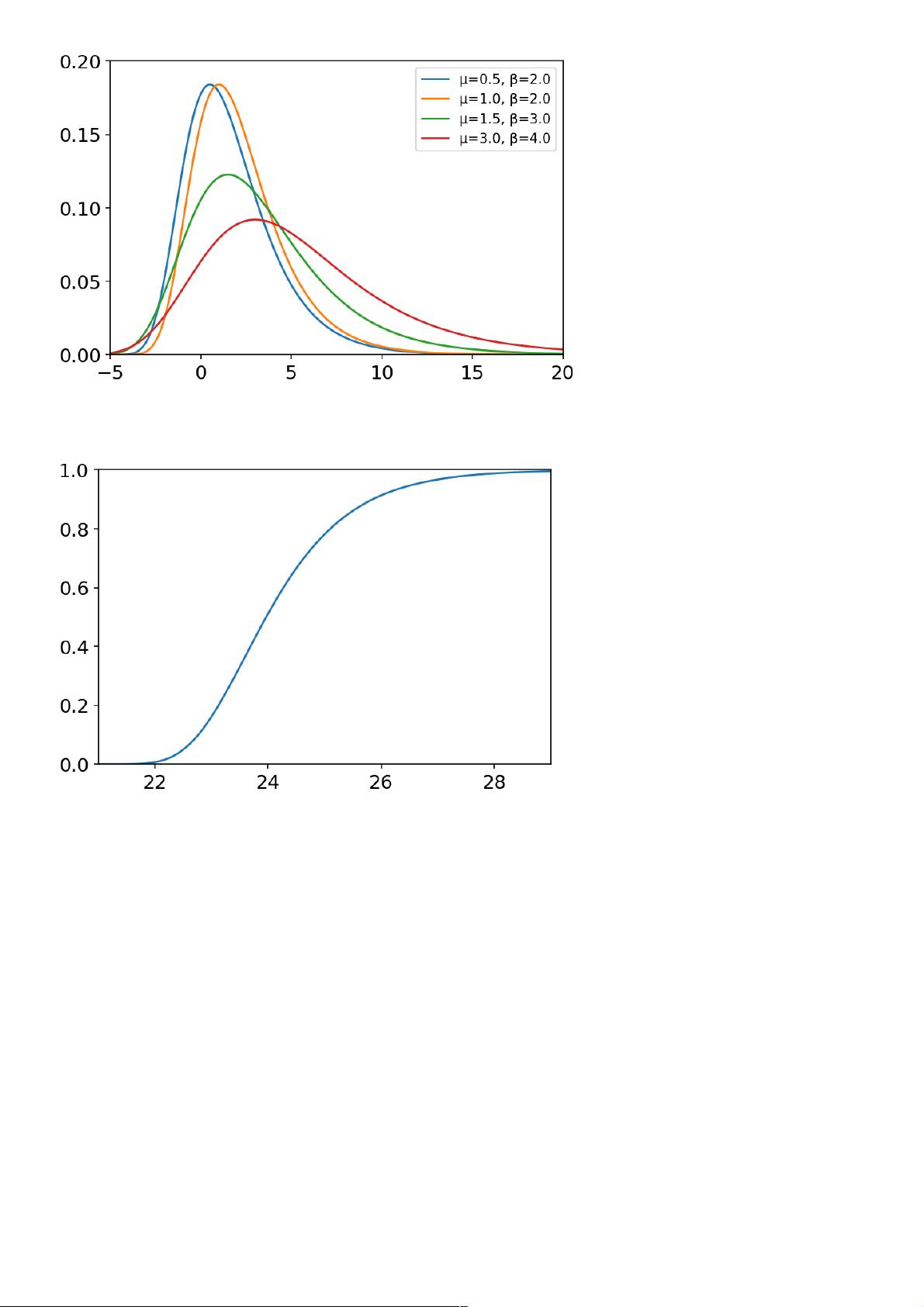
- **概率密度函数 (PDF)**:对于连续型随机变量,PDF描述了每个值出现的概率密度,如正态分布、指数分布等。
- **累积分布函数 (CDF)**:CDF是PDF的积分,它给出了随机变量小于或等于某个特定值的概率。
- **百分点函数 (PPF)**:CDF的逆函数,用于找出对应概率的值,常用于查找分布中的特定分位数。
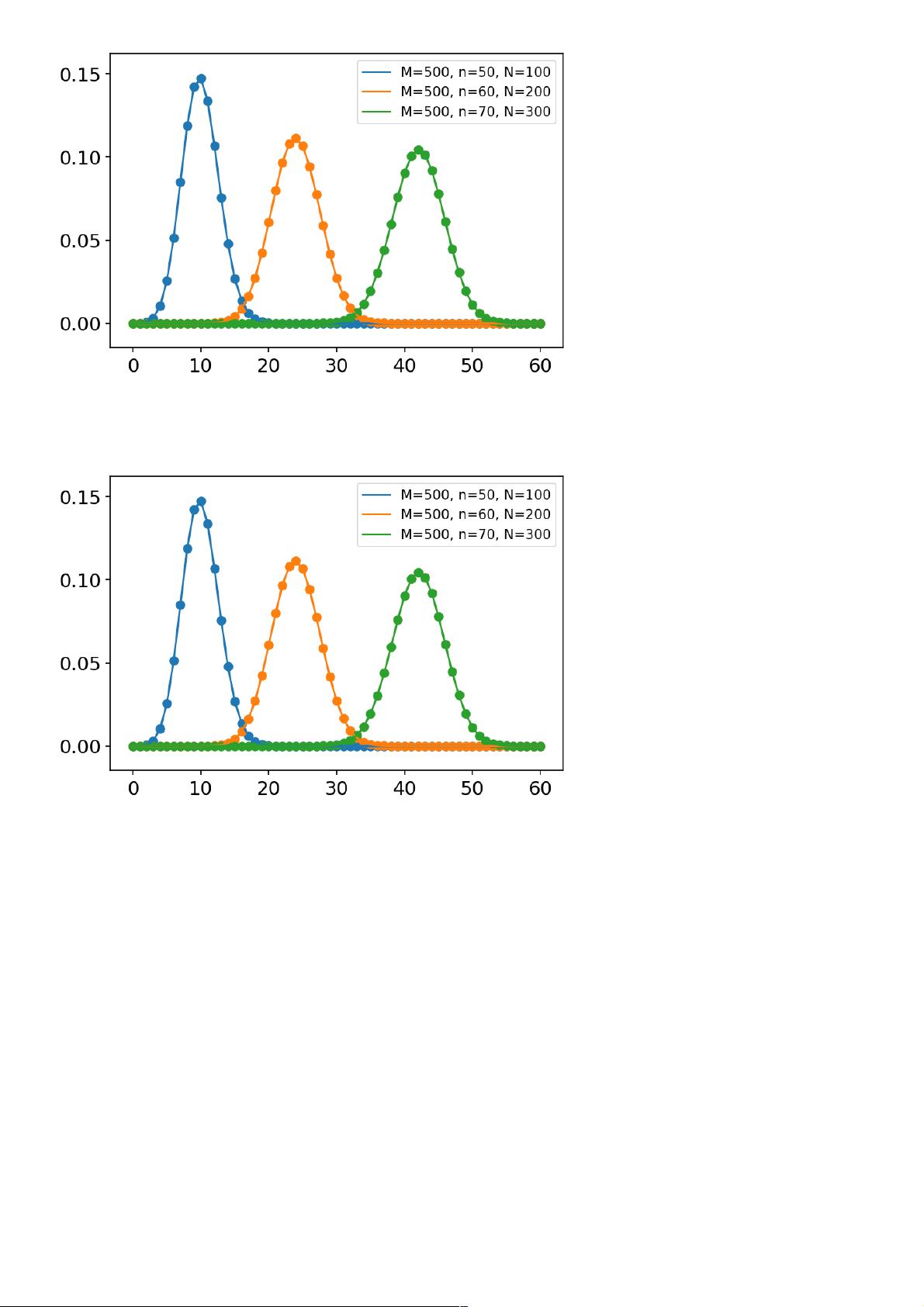
- **概率质量函数 (PMF)**:离散型随机变量的概率函数,如二项分布、几何分布等。
2. **Python实现**:
- **numpy.random.generator**:文档提到使用`numpy`库中的`Generator`类进行随机数生成,例如`integers`函数用于生成指定范围内的整数随机数,包括选项`endpoint`控制是否包含区间端点。
3. **具体概率分布**:
- **贝塔分布**:适用于0到1之间的连续随机变量,常用于比例或比例尺度的数据建模。
- **二项分布**:描述在一系列独立且成功率固定的成功失败试验中成功次数的概率分布。
- **卡方分布**:统计学中用于检验数据的自由度,也用于模型拟合。
- **狄利克雷分布**:离散概率分布,常用于描述多个分类变量的混合概率。
- **指数分布**:连续随机变量,常见于描述等待时间的模型。
4. **其他分布**:
- **F分布**:在假设检验中用于比较两个独立样本的方差比。
- **伽玛分布**:连续型分布,涉及的是非负实数的连续概率。
- **几何分布**:离散型,表示在一系列独立尝试中首次成功的次数。
- **正态分布**(高斯分布):经典连续分布,广泛应用于自然现象和数据科学中。
- **对数正态分布**:当随机变量是对数变换后的正态分布。
- **泊松分布**:离散随机变量,常用于描述事件发生次数的无记忆过程。
- **幂律分布**:在现实世界中常见,如社会网络节点度数分布等。
5. **可视化工具**:
- 文章提供了一些绘图代码,利用`matplotlib`库创建概率分布的图形,以便直观地理解和比较不同分布的特点。
通过学习本文档,读者可以掌握Python中各种概率分布的理论概念和实际应用,并能够使用numpy和scipy库进行相关的概率模拟和分析,同时了解如何将这些分布可视化,以便更好地理解和展示数据的分布特性。
955 浏览量
154 浏览量
2024-10-27 上传
2024-10-27 上传
201 浏览量
130 浏览量
339 浏览量
weixin_38588854
- 粉丝: 11
- 资源: 957