控制系统的时域分析与稳定性

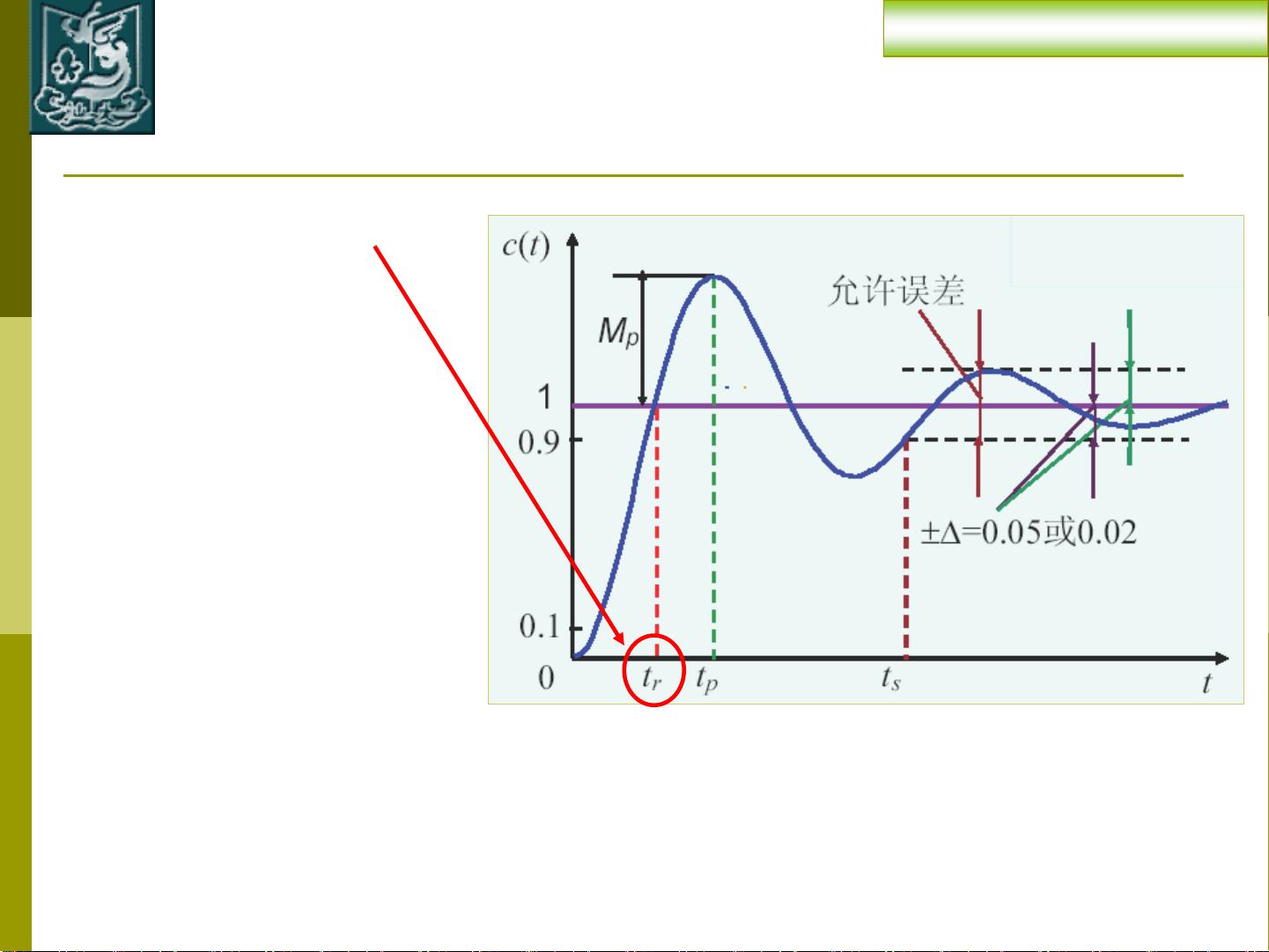
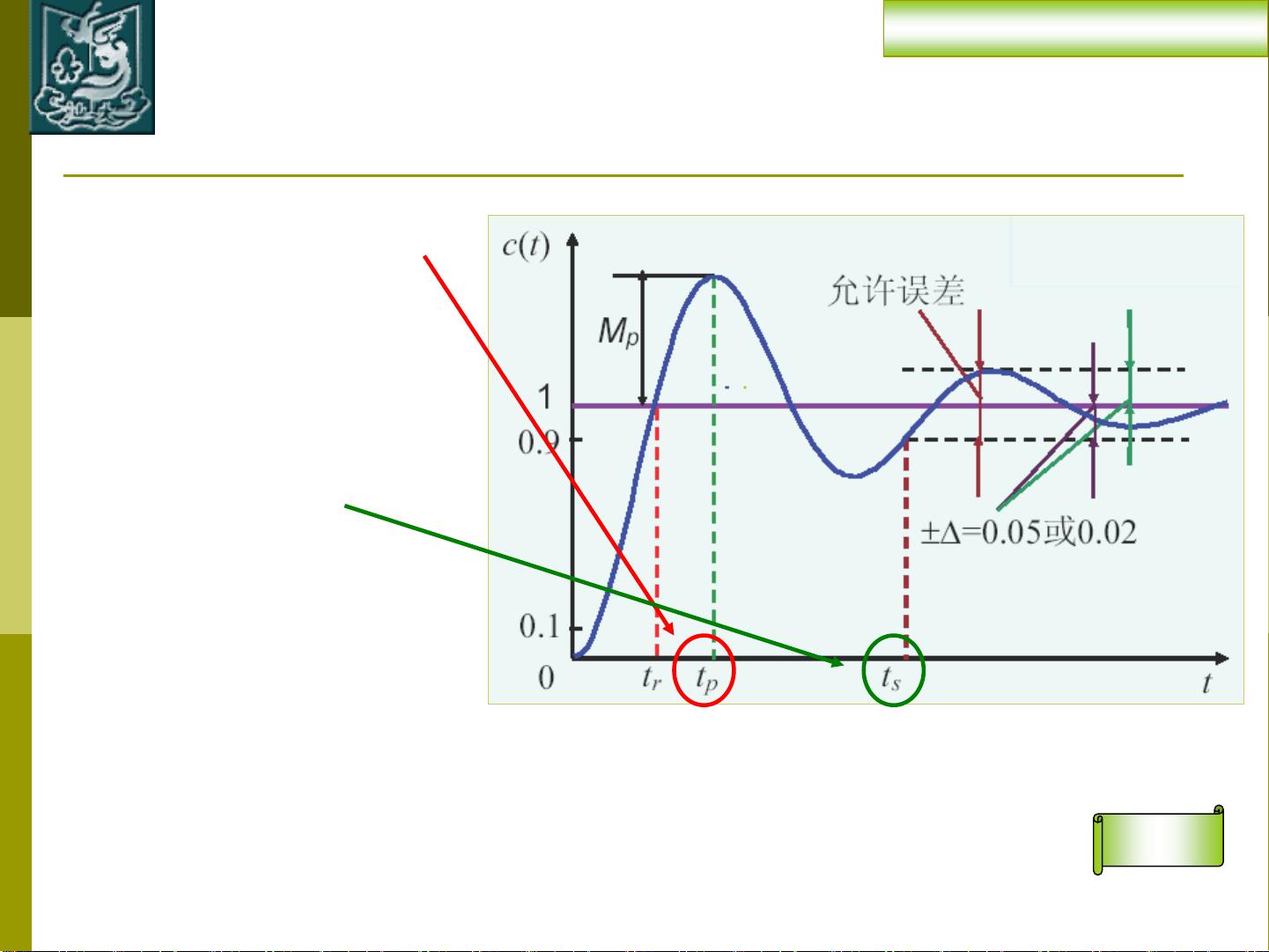
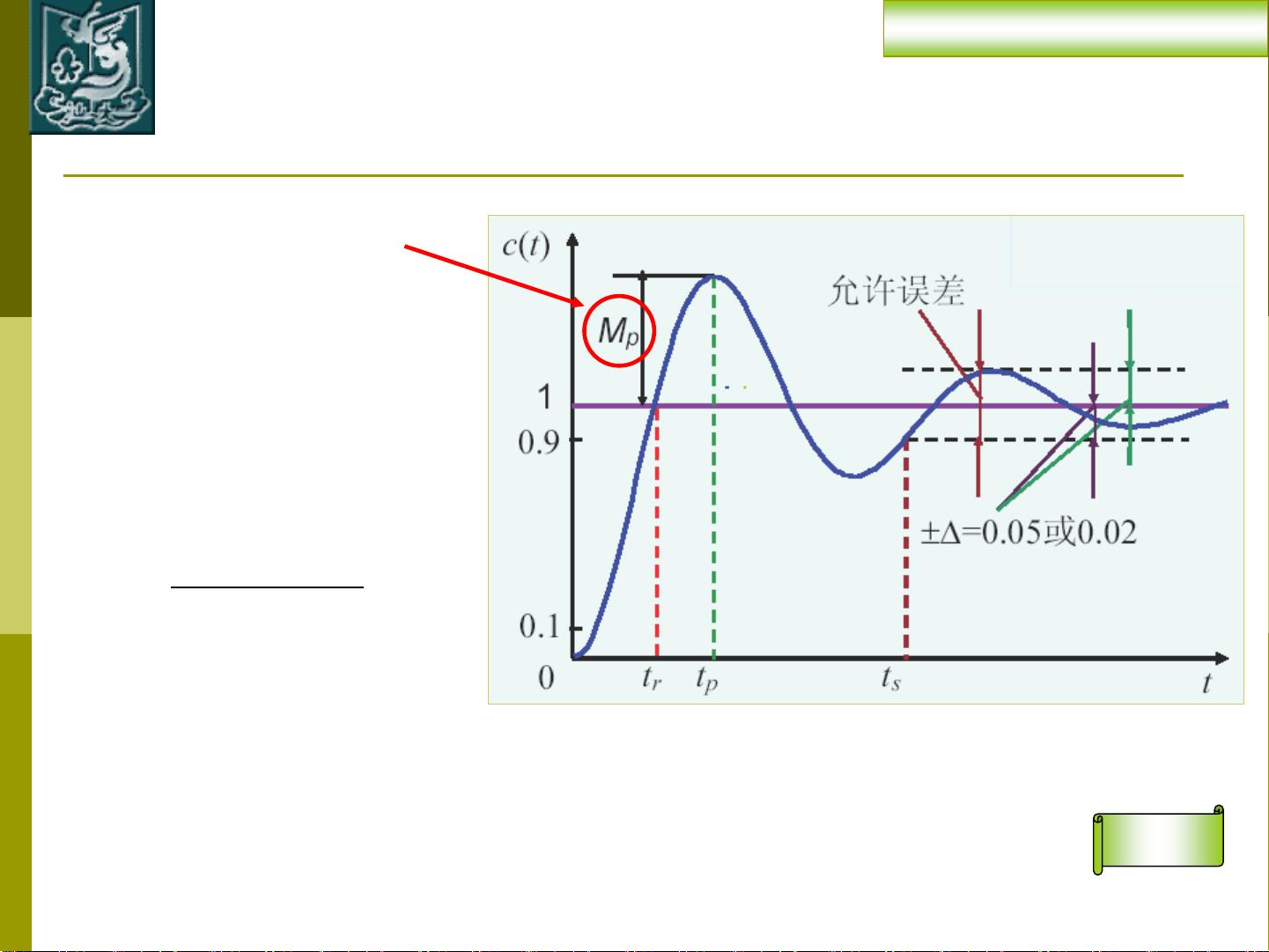
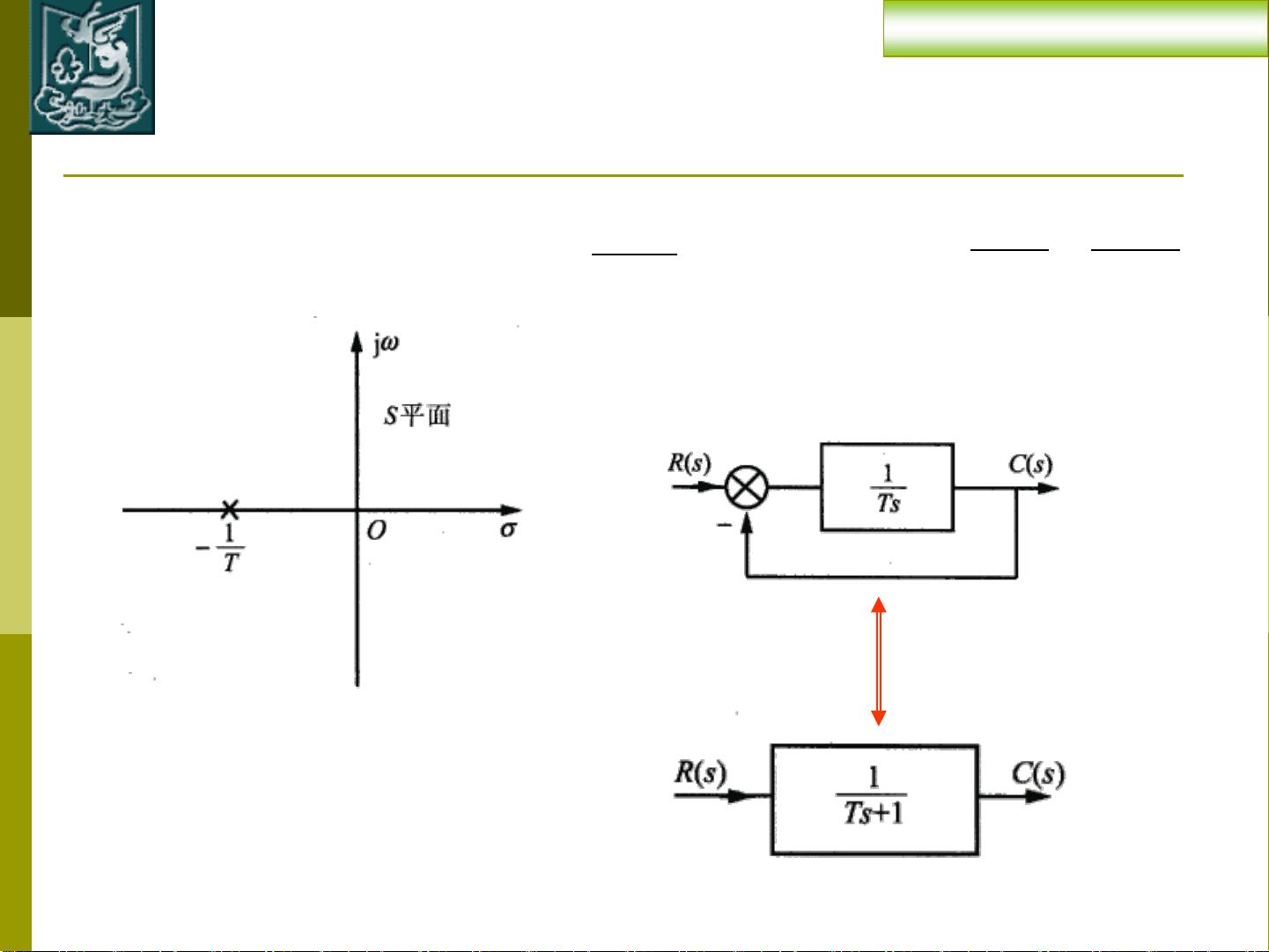
"控制系统时域分析法.pdf" 在自动控制领域，控制系统时域分析法是一种重要的分析工具，主要用于理解和评估线性定常系统的行为。时域分析关注的是系统在时间域内的响应，即输出如何随时间变化，特别是对于特定输入信号的响应。本章主要涵盖了以下几个关键知识点： 1. 典型输入信号：在分析系统性能时，通常会用到一些标准输入信号，如阶跃信号、脉冲信号、斜坡信号和正弦信号。这些信号能揭示系统在不同类型的激励下的行为。 2. 线性定常系统的时域响应和性能指标：线性定常系统遵循叠加原理，其时域响应由系统的微分方程决定。性能指标包括上升时间、峰值时间、超调量、调节时间、稳态误差等，它们用来衡量系统的响应速度、稳定性和精度。 3. 一阶和二阶系统的动态响应：一阶系统和二阶系统是最基础的动态系统模型。一阶系统通常有一个时间常数τ，决定了响应的速度。二阶系统则包含两个参数：自然频率ωn和阻尼比ζ，它们影响响应的振荡性质和衰减速率。 4. 高阶系统的动态响应：高阶系统更复杂，可能包含多个时间常数和自然频率，它们影响系统的多个时间响应特性，如多峰响应和多个振荡模式。 5. 系统稳定性分析和判据：稳定性是系统设计的核心问题。拉普拉斯变换和根轨迹法是常见的稳定性分析工具。系统稳定的判据包括劳斯判据、赫尔维茨判据和奈奎斯特判据，这些判据基于系统传递函数的特征根或奈奎斯特图来确定系统的稳定性。 6. 稳态误差的定义和计算：稳态误差是指系统在长期运行后，输出与期望值之间的差异。它分为最终稳态误差和稳态误差系数，与系统结构和增益有关，是衡量系统跟踪能力的关键指标。 时域分析不仅提供了系统动态行为的直观理解，还为系统设计和优化提供了基础。通过时域分析，工程师可以调整系统参数以满足特定的性能要求，如快速响应、低超调和小稳态误差。此外，它还能帮助识别系统中的不稳定因素，从而进行相应的补偿设计。在实际工程应用中，时域分析与频域分析相结合，能够全面地理解控制系统的性能。