MATLAB数值微积分：极限与导数计算实例

MATLAB数值微积分是计算机科学与工程领域中的一个重要工具，它在处理数学问题时，特别是在没有精确解析解的情况下，提供了近似计算极限和导数的能力。在MATLAB中，求解极限和导数通常采用差分和梯度函数。 4.1 节主要介绍了两种核心概念：差分和梯度计算方法。 1. **差分**： - `diff(X)` 函数用于计算一阶差分，对向量 `X`，结果是将相邻元素相减得到的差数组，例如对于一维向量 `X`，`Dx = X(2:n)-X(1:n-1)`，这意味着 `Dx(i)` 是 `X` 中第 `i+1` 个元素与第 `i` 个元素的差。 - 对于二维矩阵 `X`，`DX = X(2:n,:) - X(1:n-1,:)`，则返回的是沿着行的方向进行的差分。 - `diff(X,N,DIM)` 允许指定沿特定维度 `DIM` 进行 N 阶差分，如果 N 大于该维度的大小，则返回空数组。 2. 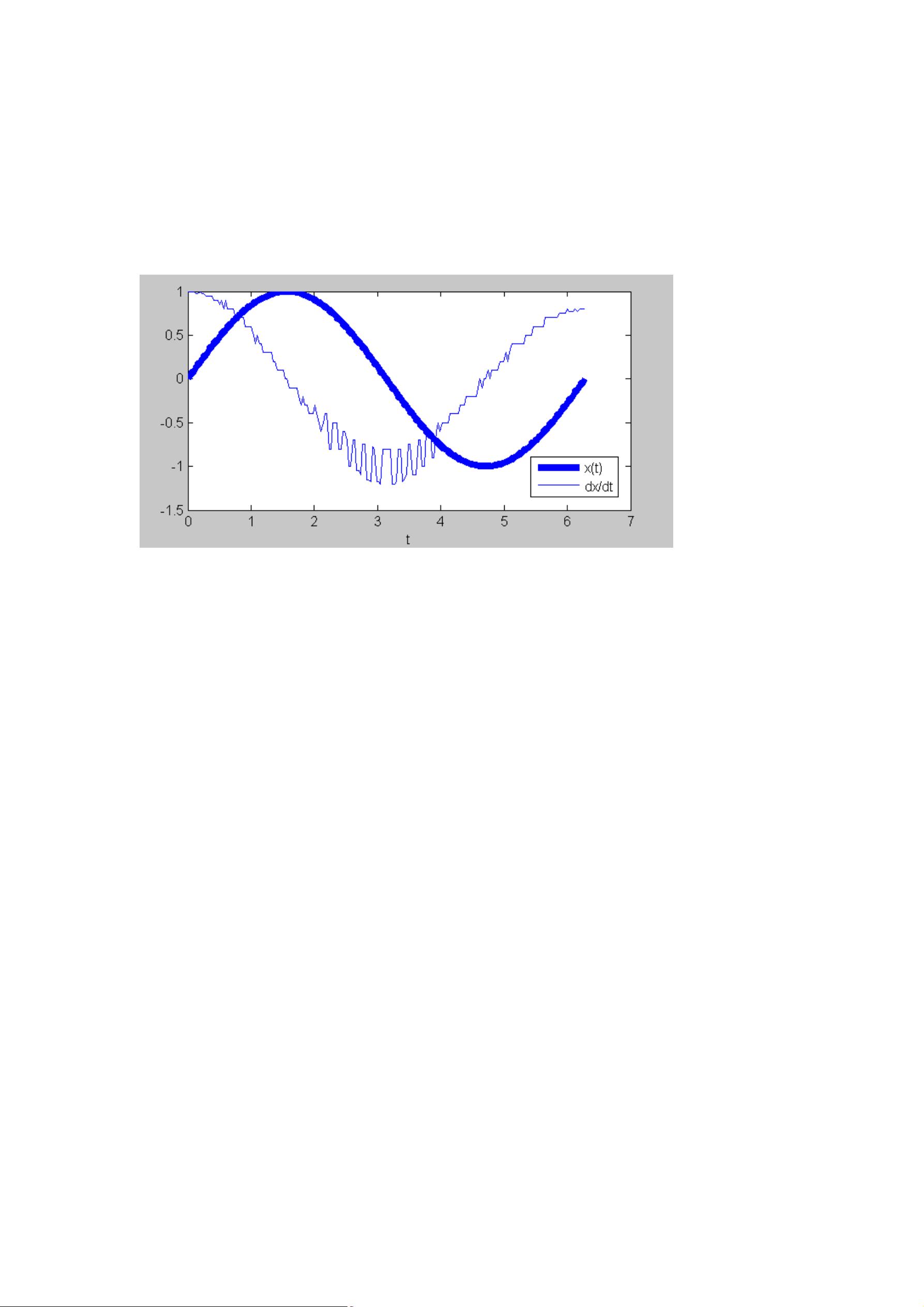**梯度**： - `gradient(F)` 计算函数 `F` 的梯度向量，它返回一个与输入函数 `F` 同维的向量，表示每个元素处的切线斜率。例如，对于矩阵 `F`，`FX = gradient(F)` 按行计算，而 `FX_2, FY_2 = gradient(F, 0.5)` 则以采样间隔 0.5 进行计算。 - 在示例中，`f1` 和 `f2` 分别是两个函数，`L1` 和 `L2` 是分别用数值方法计算 `lim f(x)` 和 `lim (f(x)/x)` 当 `x` 接近 0 时的近似值，但需要注意的是，数值方法可能会因为精度问题导致错误的结果，如 `L1` 应为 0 而非给出的 0。 数值微积分在MATLAB中主要用于求解理论难以处理或无法精确解析的极限和导数问题，它在优化、信号处理、物理学等许多领域都有广泛应用。理解并熟练掌握这些基本操作，能够大大提高处理复杂数学问题的效率。当面对极限和导数计算时，结合符号计算 `sym` 可以提供更精确的结果，避免数值计算带来的误差。