倒立摆控制方法研究：从经典到智能

"基于matlab的倒立摆仿真.doc" 倒立摆是一种经典的控制理论研究对象，因其独特的动态特性，如非线性、不稳定和多变量耦合，长期以来一直是控制系统设计和优化的重要实验平台。在本文中，我们将深入探讨基于MATLAB的倒立摆仿真以及目前倒立摆控制理论的几种主要方法。 首先，我们关注经典控制理论。一级倒立摆的控制可以通过分析力学模型，应用牛顿第二定律建立非线性运动方程，然后线性化并进行拉普拉斯变换来设计控制器。经典的PID控制或频率域设计方法可以用于一级倒立摆，通过适当的反馈确保闭环系统的稳定性。然而，这种方法对更复杂的多级倒立摆（如二级或三级）的控制效果有限。 现代控制理论，特别是H_∞状态反馈，提供了一种更灵活的控制策略。这种方法涉及建立倒立摆的状态空间模型，结合H_∞控制和卡尔曼滤波，以实现对系统性能的优化。此外，文献中提到的极点配置、LQR（线性二次型最优控制）和LQG（线性二次型-高斯最优控制）等状态反馈方法也被证明在一级倒立摆控制中有效，并且在某些情况下，对二级倒立摆也有良好的控制效果。 面对倒立摆的非线性和不确定性，智能控制理论，尤其是模糊控制，已经成为研究热点。模糊控制能够处理不确定性和模型不精确性，通过定义模糊规则和推理过程，实现对一级和二级倒立摆的有效控制。大量实验表明，模糊控制器能够在没有精确系统模型的情况下，提供稳定的控制性能。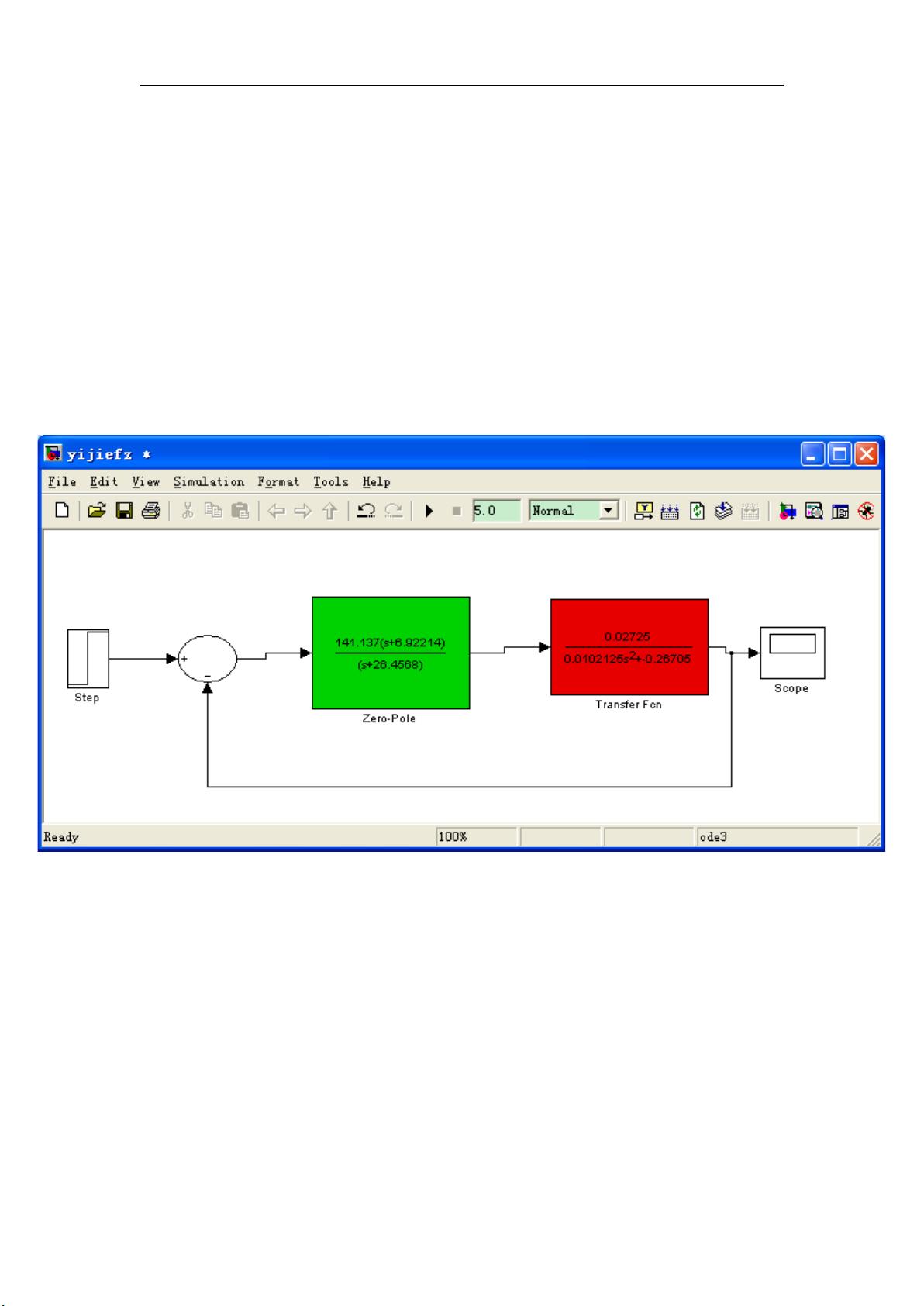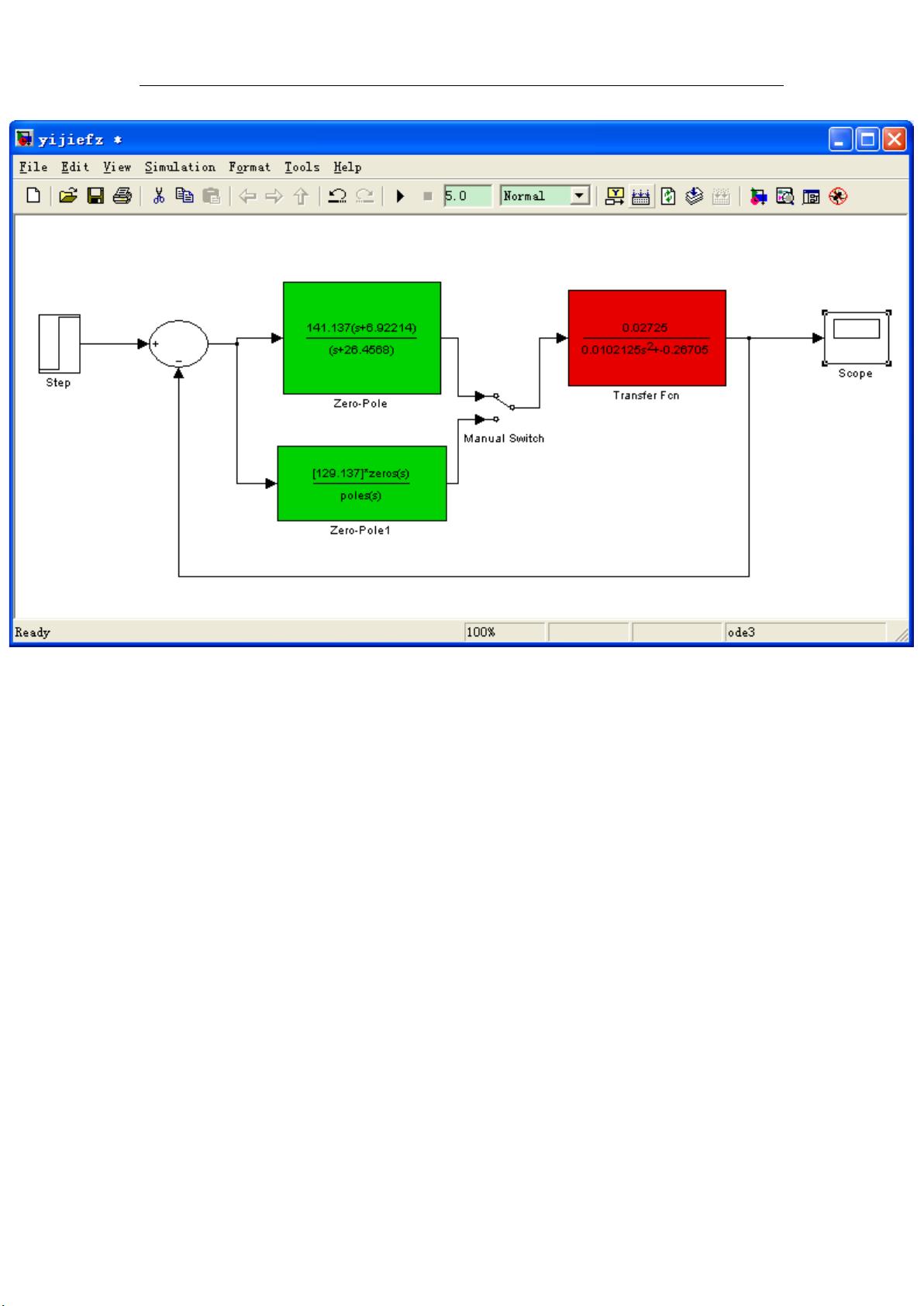 MATLAB作为一个强大的数值计算和仿真平台，为倒立摆控制系统的建模、分析和设计提供了便利。通过Simulink模块，可以构建动态系统模型，模拟不同的控制策略，观察系统响应，并进行参数优化。这使得研究人员能够在理论研究和实际实现之间架起桥梁，推动控制理论的发展。 基于MATLAB的倒立摆仿真为研究和测试各种控制理论提供了一个实用的工具，无论是经典控制、现代控制还是智能控制。通过不断的仿真和实验，我们可以更好地理解和改善倒立摆的稳定性，同时推动控制理论在更广泛的工程应用中的进步。