非线性振动特性：固有频率与振幅关系及混沌运动

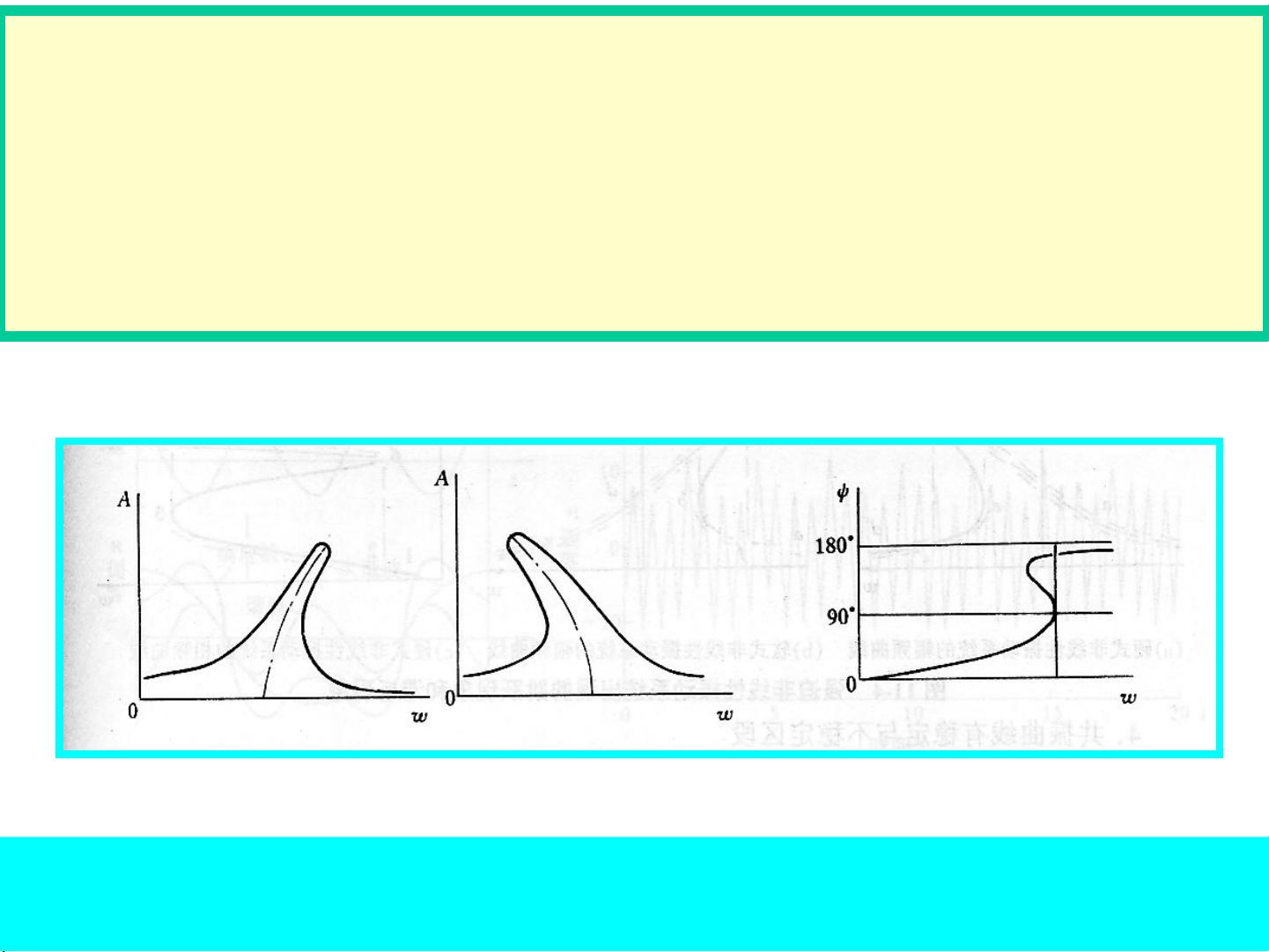
"非线性振动第11章.ppt - 非线性振动院士课件" 在动力学领域，非线性振动是研究的重要主题。非线性振动系统的特点在于，它们的动态行为与振幅、频率等因素密切相关，这与线性振动系统的简单特性截然不同。以下是对第11章非线性方程解的某些物理性质的详细解释： 1. 当恢复力为非线性时，固有频率不再是常数，而是振幅的函数。以杜芬方程为例，该方程包含了位移的三次方项，其固有频率会随着振幅A的变化而改变。对于分段线性系统，固有频率表达式也反映出这种依赖关系，即固有频率可以是振幅的函数，具体形式由系统参数决定。 2. 非线性振动系统的共振曲线具有独特的特性。与线性系统中单一峰值的共振曲线不同，非线性系统的共振曲线可能呈现出多峰、分岔或不稳定性。这种差异主要源自非线性恢复力的影响。 3. 强迫非线性振动系统中存在滞后与跳跃现象。当外部激励频率接近系统固有频率时，振动状态可能突然跳跃至另一个振幅水平，这是由于非线性效应导致的相位滞后和振动状态的不连续变化。 4. 共振曲线的稳定与不稳定区段。非线性振动系统中的共振曲线可能存在稳定的振动区域，以及随着参数变化而变得不稳定的区域。这种现象在系统设计和控制中具有重要意义。 5. 超谐波响应和次谐波响应是强迫振动系统的一个特征。除了与激励频率相同的谐波成分外，系统还可以产生高于或低于激励频率的谐波成分，这在线性系统中是不存在的。 6. 在多个简谐激振力作用下，非线性振动系统会发生复杂的组合振动。这意味着振动模式可以是多个简谐振动的组合，形成丰富的频谱结构。 7. 非线性振动系统的叠加原理不再适用。线性系统中，小振幅振动的叠加遵循叠加原理，但在非线性系统中，这个原则失效，因为大振幅振动的效应不能简单地通过小振幅振动的叠加来预测。 8. 频率俘获是非线性振动系统中的一个特殊现象。在某些条件下，系统可能会锁定到特定的频率，即使外部激励频率发生变化，系统仍保持在原来的振动频率。 9. 自激振动是某些非线性系统可能出现的行为，即使没有外部激励，系统也能维持振动，这通常与系统内部的能量转换机制有关。 10. 混沌运动是高度复杂的非线性行为，非线性振动系统在某些参数组合下可能表现出混沌，这是一种看似随机但实际上是确定性的动态行为。 通过图11-1，我们可以直观地看到固有频率与振幅之间的关系：硬式非线性系统（固有频率随振幅增大而增加）和软式非线性系统（固有频率随振幅增大而减小）。图11-2展示了通过实验获取的振动曲线，帮助我们区分硬式和软式非线性振动系统。 非线性振动的研究涵盖了广泛的现象和复杂的动力学行为，这对于理解和控制各种工程系统，如机械、航空航天、土木结构等，具有重要的理论和实践价值。深入理解这些非线性特性对于优化系统设计、避免潜在的破坏性振动以及开发新的控制策略至关重要。