回溯策略详解：算法思想与货郎问题解决实例

"本文主要介绍了五大常见算法策略之一的回溯策略，并以货郎问题为例进行详细阐述。回溯策略是一种基于树形结构的解空间搜索方法，当搜索到某个节点不满足条件时，会回溯尝试其他路径。货郎问题要求在一个无向带权图中找到一个包含所有城市的最短环路。通过构建解空间树并进行深度优先搜索，可以找到最短路径。文章提供了Java代码实现，以帮助理解回溯策略的基本思想和应用。" 在计算机科学中，回溯策略是一种用于解决优化问题和组合问题的有效方法。它通过搜索问题的所有可能解来找到符合条件的解，当发现当前路径无法导致有效解时，会撤销之前的选择，退回一步去探索其他可能性。回溯策略通常与深度优先搜索（DFS）相结合，因为它能有效地处理那些具有大量分支的搜索树。 货郎问题，又称为旅行商问题（Traveling Salesman Problem, TSP），是一个经典的组合优化问题。在这个问题中，一个推销员需要访问n个城市，并且最后返回起点，目标是找到一条经过每个城市一次且总距离最短的路线。这个问题是NP完全问题，意味着没有已知的多项式时间算法可以在所有输入实例上找到最佳解。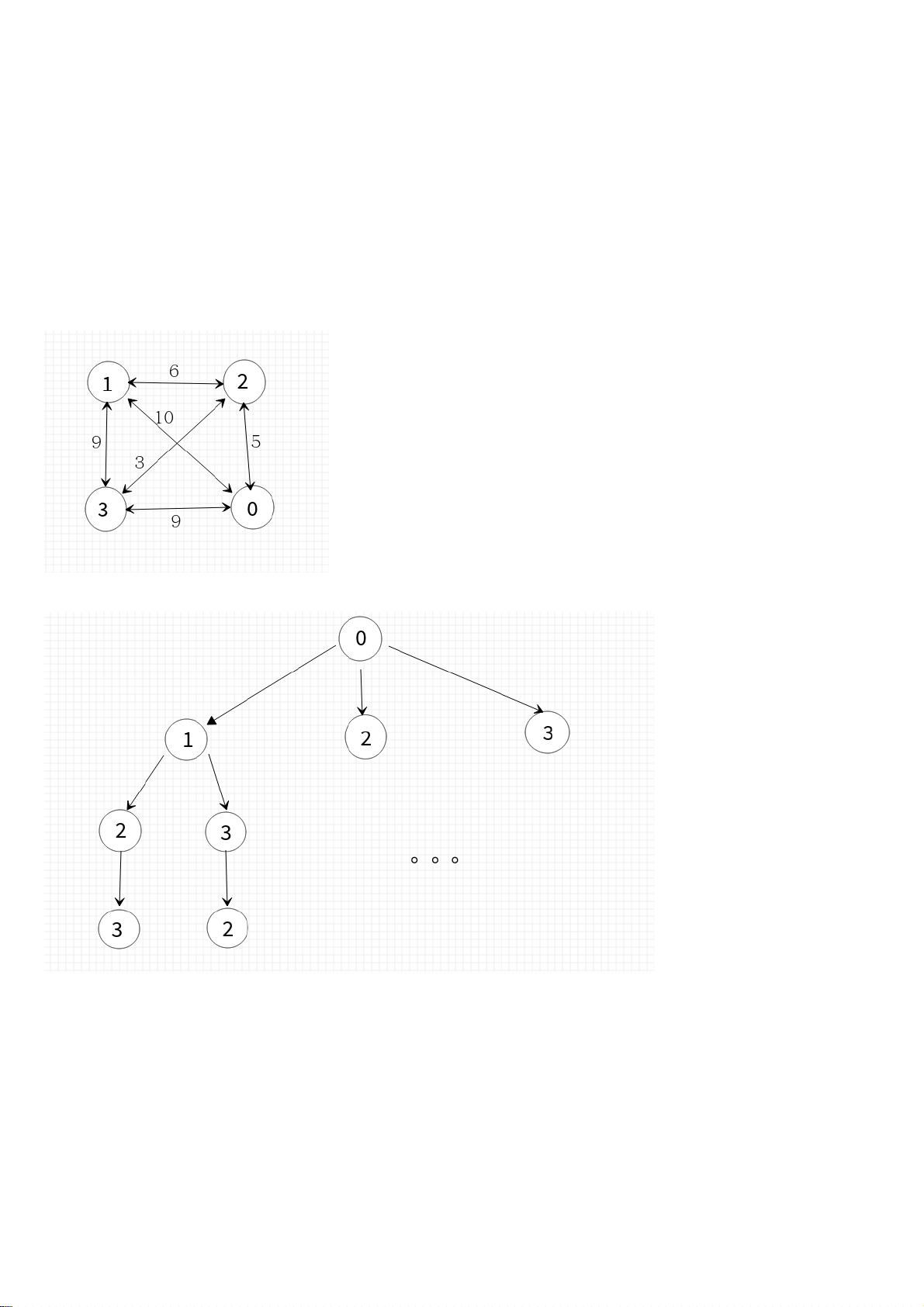 在给定的例子中，我们有一个4个城市组成的网络，每个城市间的距离用邻接矩阵表示。为了解决货郎问题，我们创建一个解空间树，每个节点代表一种可能的路径选择，而边则表示城市之间的连接。我们使用回溯策略，从0号城市开始，沿着深度优先搜索的路径前进，每到达一个新的城市，就更新路线并计算当前路径的总距离。如果在某一步发现总距离超过了已知的最短距离，我们就回溯到上一步，尝试不同的路径。 Java代码示例展示了如何实现这个回溯策略。变量`city`记录每个城市的访问状态，`road`数组保存了旅行的顺序，`Min`用来记录当前找到的最短路径长度。`travel`函数递归地遍历所有可能的路径，直到找到最短路径。在函数中，`level`表示当前所在的城市位置，`len`是当前路径的总长度。当到达最后一个城市时，检查当前路径的总长度是否小于已知的最短路径，如果是，则更新最短路径。 回溯策略在解决诸如八皇后问题、数独问题、迷宫问题等许多组合优化问题时都非常有用。它能够避免无效的分支，通过剪枝减少搜索空间，提高算法效率。然而，对于大规模问题，回溯策略可能会变得效率低下，因为其时间复杂度通常是指数级的。因此，在实际应用中，可能会结合其他算法如动态规划或近似算法来提高解题效率。