硅/III-V异质集成技术下的窄线宽半导体激光器进展教程
下载需积分: 17 | PDF格式 | 7.35MB |
更新于2024-06-30
| 72 浏览量 | 举报
激光器线宽测试是衡量激光器性能的关键参数之一，它反映了光辐射的频率稳定性。线宽越窄，意味着激光输出的单色性越好，对于通信、精密测量等领域具有重要意义。本文主要关注的是外腔窄线宽激光器的发展，特别是通过硅/III-V族异质集成技术实现的进展。
在半导体激光器中，线宽测试通常涉及到对激光光谱进行分析，以确定其强度随频率的变化程度。这一过程涉及到的技术包括傅里叶变换光谱分析（FTIR）、光谱扫描或利用高分辨率光谱仪测量激光的自发发射或受激发射谱。窄线宽激光器的研究重点在于减少自发辐射噪声和机械振动等因素引起的线宽拓宽，以实现更高的稳定性和相干性。
文章《APLPhotonics》(2019年4,111101)详细介绍了利用Si/III-V异质集成技术制造窄线宽可调谐半导体激光器的方法。这种技术结合了硅基芯片的低成本和高性能与III-V族材料如砷化镓等的优良光学特性，如更高的量子效率和较低的阈值电流。通过这种集成方式，可以实现激光器的优化设计，例如减小热效应对线宽的影响，并提高激光器的温度稳定性和调谐能力。
文章作者Minh A. Tran, Duanni Huang, 和 John E. Bowers在文中探讨了这种方法在当前硅光子学领域之外的潜力，以及它如何推动Hybrid Integration beyond Silicon Photonics这一特殊主题的发展。他们强调了这种异质集成技术对于量子点光子集成电路未来发展的前景，指出它可能为光通信系统提供更高效、低噪声的光源。
此外，文章还提到了其他相关研究，如关于低噪声、可调谐的硅光子激光器的综述，以及关于混合和异质光子集成的最新进展。这些研究共同展示了在不断追求光辐射纯度和稳定性方面所取得的进步，这对于现代信息技术，如数据中心通信、精密测量仪器和量子计算等领域的发展具有重要意义。
这篇文章提供了深入理解外腔窄线宽半导体激光器研发现状及前景的重要资源，特别强调了异质集成技术在实现这些高性能激光器中的关键作用。通过阅读和参考这些内容，研究人员和工程师可以更好地了解如何优化和设计下一代光子学器件，以满足日益增长的高性能应用需求。
APL Photonics
TUTORIAL
scitation.org/journal/app
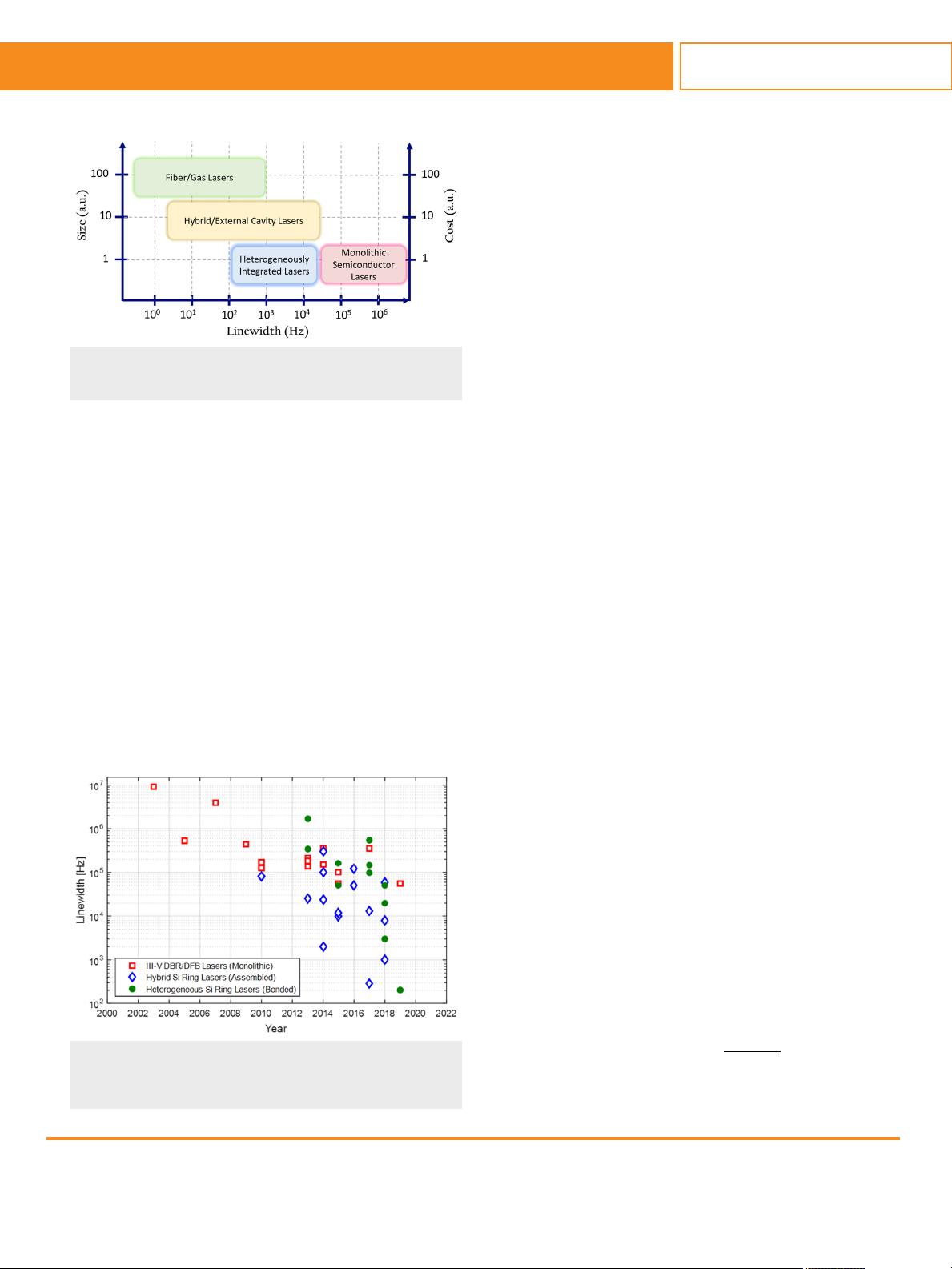
FIG. 2. Summary of the general metrics for narrow linewidth lasers. Heteroge-
neously integrated lasers have the potential to match hybrid and external cavity
lasers in performance without an increase in size and cost.
external cavity lasers using semiconductor gain chips with long, low-
loss optical delays are used. These external cavities are comprised
of fibers or external crystalline whispering gallery resonators and
Fabry-Perot etalons.
55–57
More recently, integrated external cavities
using the aforementioned hybrid integration to assemble multiple
semiconductor chips have been used to further reduce the cost and
size of such lasers.
58–62
Here, the superior passive performance of sil-
icon or silicon nitride waveguides has a direct benefit in reducing the
noise of the laser. In this work, heterogeneously integrated lasers are
shown to provide much of the same benefits in terms of linewidth
reduction, while maintaining cost and footprint similar to mono-
lithic III-V semiconductor lasers. These relevant metrics are given
in Fig. 2, and a number of results are highlighted in Fig. 3. State of
the art heterogeneous silicon/III-V lasers, some of which will be pre-
sented in this tutorial, have exceeded the best of the monolithic III-V
lasers in some aspects, such as laser linewidth and tuning range.
The outline of this tutorial is as follows: In Sec. II, we provide
a formal definition of laser phase noise and spectral linewidth as
FIG. 3. Progress in Lorentzian linewidth of semiconductor lasers over the past
two decades. While monolithic lasers have not improved beyond 50 kHz or so,
hybrid and heterogeneous silicon lasers have pushed Lorentzian linewidths to
subkilohertz levels in recent years.
used in the context of this tutorial. We discuss techniques to accu-
rately characterize the linewidth of the laser. In Sec. III, we discuss
the fundamental techniques behind linewidth reduction in lasers.
We classify lasers as either solitary cavity lasers in which there is
only a single section or extended cavity lasers in which there is a
passive section longitudinally coupled to the gain section. We out-
line basic design methodology that can be used to achieve the nar-
row linewidth in each case. In Sec. IV, we provide some examples
of heterogeneous silicon/III-V lasers that have been optimized for
the narrow linewidth. We discuss distributed feedback (DFB) lasers,
narrowly tunable distributed Bragg reflector (DBR) lasers, as well as
widely tunable ring resonator-based lasers. The design methodolo-
gies covered in Sec. III are applied to each type of laser, and results
are shown. Finally, we identify areas in which further improvements
are needed in Sec. V. We investigate techniques at the system level
such as laser stabilization, as well as exploratory concepts that can
improve the laser at the device level.
II. FREQUENCY NOISE AND SPECTRAL LINEWIDTH OF
SEMICONDUCTOR LASERS
This section provides readers with a brief summary on some
technical terms and measurement methods commonly used to char-
acterize and benchmark the laser noise and spectral purity. In
Sec. II A, we discuss the link between frequency noise characteris-
tics of the laser to its spectral line shape and linewidth. In Sec. II B,
we discuss measurement methods for precise laser noise/linewidth
characterization. Within the scope of this paper, lasers are single
frequency.
A. Basics of frequency noise and spectral line shape
Below the relaxation oscillation frequency, the frequency noise
spectrum of a free-running semiconductor diode laser typically fea-
tures two distinct frequency ranges with different characteristics.
At the lower frequency range, the noise spectrum is dominated by
various 1/f noises which decay with frequency following 1/f
α
with
α >0, as shown in Fig. 4(a). Other kinds of “technical noises” that
originate from sources external to the laser could also meddle in the
low frequency range. At higher frequencies where the 1/f noises and
other technical noise die out, the white noise caused by the random
processes of spontaneous emission and carrier fluctuations becomes
dominant.
The laser optical field power spectral density, or laser “spec-
tral line shape,” can directly be found from the laser frequency noise
by integrating over the full range of Fourier frequency,
63,64
as given
in Eq. (1), where ν
0
is the laser’s center optical frequency, S
E
(ν) is
the optical power spectrum density (PSD) at optical frequency ν, E
0
is the amplitude of optical field (assumed to be constant as ampli-
tude noise is neglected), and S
ν
(f ) is the frequency noise PSD at the
Fourier frequency f,
S
E
(ν)=E
2
0
∫
∞
0
cos[2π(ν −ν
0
)τ]
×exp−4
∫
∞
0
S
ν
(f )
sin
2
(πf τ)
f
2
df dτ. (1)
Although not analytically solvable in general cases, it has been shown
that the typical spectral shape of a laser is dominantly determined
APL Photon. 4, 111101 (2019); doi: 10.1063/1.5124254 4, 111101-3
© Author(s) 2019
剩余19页未读，继续阅读
相关推荐
