动态规划解多段图问题

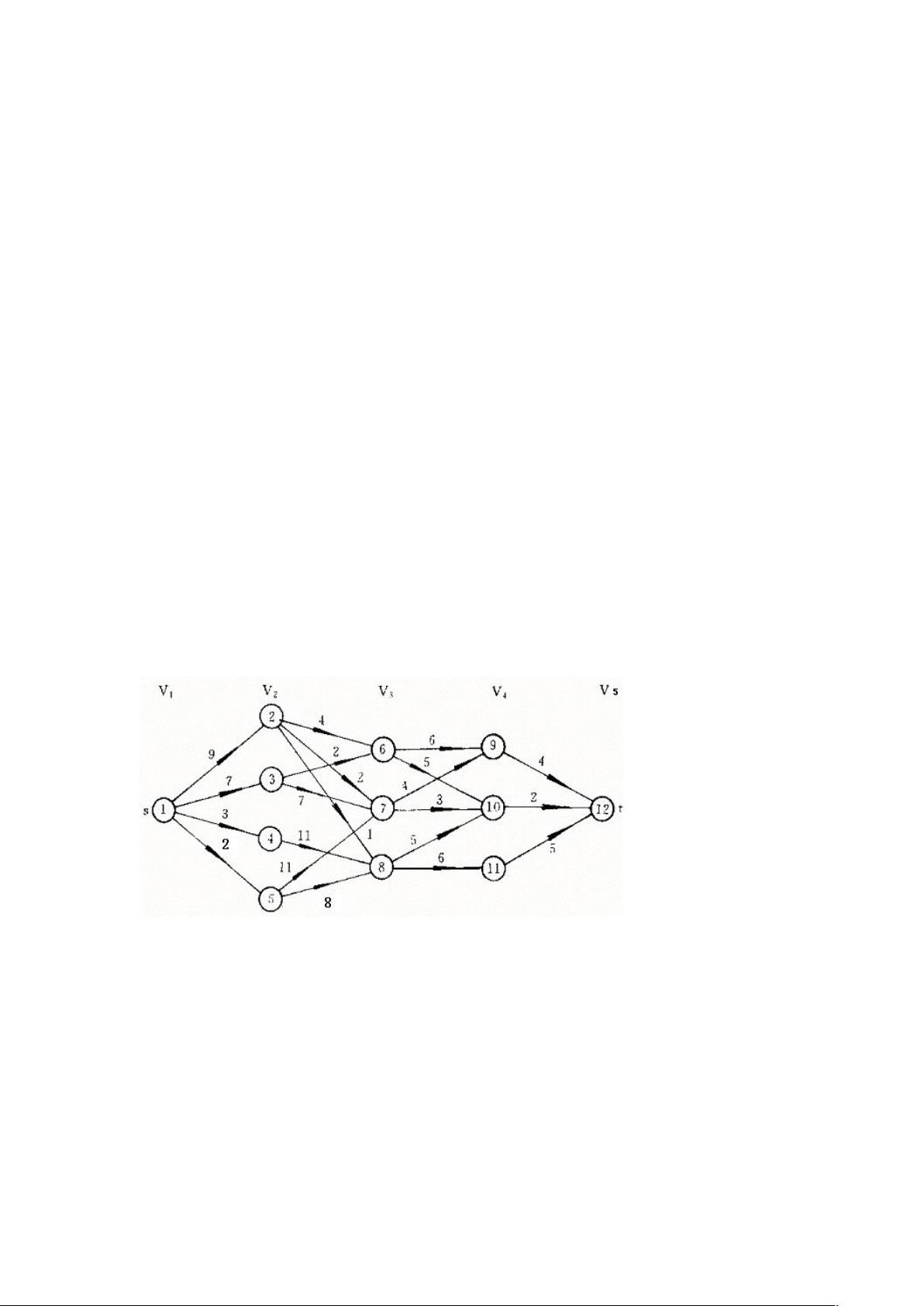
"这个资源包含关于多段图问题的算法研究，包括源代码和报告，旨在通过动态规划方法解决这类问题。动态规划是基于最优子结构和子问题重叠性质的一种算法设计策略，由Richard Bellman在50年代提出。实验内容聚焦在赋权有向多段图上，寻找源点s到汇点t的最短路径。算法分析部分证明了最优化原理对多段图的适用性，并给出了动态规划方程来计算最小成本路径。" 在多段图问题中，动态规划是一种有效的解决方案。动态规划的核心思想是将复杂问题分解为多个相互关联的子问题，通过解决这些子问题来构建整个问题的最优解。在这个问题中，图的顶点被分为多个不相交的子集，源点s位于第一子集，汇点t位于最后一子集，所有的边连接相邻子集的顶点。动态规划的适用性取决于问题是否存在最优子结构和子问题的重叠。 最优子结构意味着原问题的最优解包含其子问题的最优解。在多段图问题中，如果已经确定了从源点s到某个中间节点vi的最优路径，那么接下来只需要找到从vi到汇点t的最短路径，这两部分组合起来就是s到t的最短路径。 子问题的重叠是指在解决问题的过程中，某些子问题会被重复计算。在多段图中，当逐步求解从不同节点到汇点的最短路径时，可能会遇到相同的子问题。动态规划通过存储和重用这些子问题的解，避免了重复计算，提高了效率。 在算法分析中，通过反证法证明了最优化原理对多段图问题成立。如果一条从s到t的最短路径不包含某个中间节点vi的最优路径，那么可以构造一条更短的路径，这与最短路径的定义矛盾，从而证明了最优性原理。 动态规划方程通常用于描述这一过程，设P(i, j)表示从子集Vi中的节点j到汇点t的最小成本路径，COST(i, j)为该路径的成本。方程定义了如何从子集Vi+1开始递归地计算到达汇点的最小成本，最终得到从源点s到t的最短路径。 这个资源提供的内容深入探讨了动态规划在解决多段图问题中的应用，不仅提供了理论分析，还包含了实际的源代码和报告，为学习者提供了一个全面理解动态规划和多段图问题的实践平台。