布尔代数与逻辑电路基础：构建与门、或门与加法器

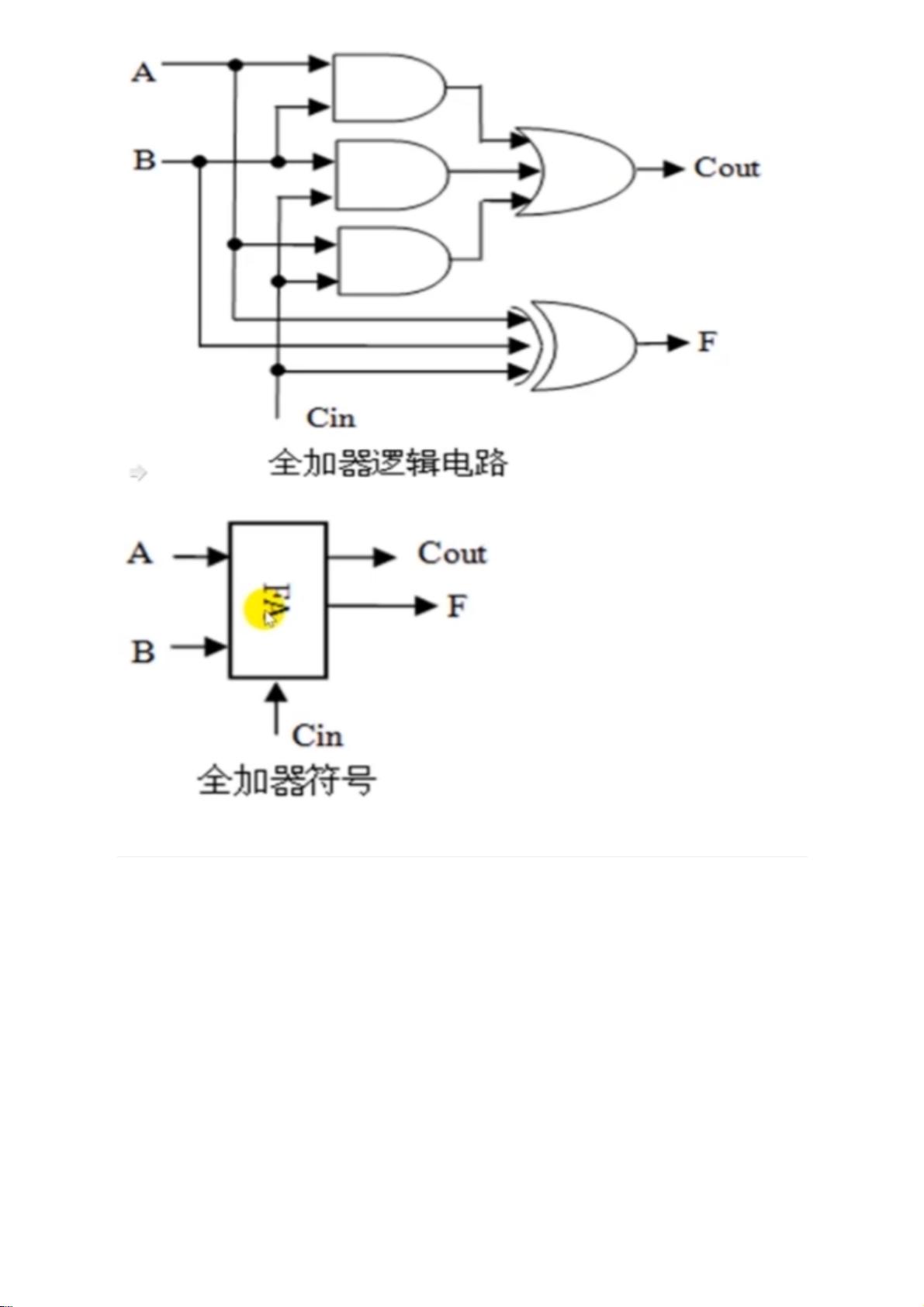
本篇课堂笔记主要介绍了布尔代数及其在逻辑电路设计中的应用。布尔代数是一种数学理论，它将逻辑运算简化为基于0和1的运算规则，这是由19世纪英国数学家乔治·布尔开创的。布尔运算包括与（AND）、或（OR）、非（NOT）三种基本操作，它们分别对应着逻辑“与”、“或”和“非”概念，使用的运算符分别是“·”、“+”和“￣”。 逻辑门电路是实现布尔运算的核心组件，包括与门、或门和非门。这些基本门电路可以通过组合形成更复杂的逻辑电路，如异或门。对于n位逻辑运算，需要使用n个相同的门电路进行并行处理，例如，按位与、或和异或都是基于每位输入的独立运算。 逻辑电路进一步分为组合逻辑电路和时序逻辑电路。组合逻辑电路不具有记忆功能，输出仅依赖于当前输入；而时序逻辑电路则包含存储单元，其输出不仅受当前输入影响，还取决于先前的状态，这使得它们能够实现计数器和触发器等复杂功能。 课堂中还提及了如何设计和实现特定功能的逻辑部件，如译码器、编码器、多路选择器和加法器。例如，多路选择器（MUX）用于根据控制信号选择多个输入中的一个输出，其中k路选择器的控制端S位数与输入路数有关，为log2k。一位加法器，特别是全加器，是构建n位加法器的基础，通过串连多个全加器实现多位加法。对于带符号整数的加减运算，由于溢出问题，通常需要额外的标志位或通过减法来辅助判断。 最后，算术逻辑部件（ALU）在计算机中扮演关键角色，它负责无符号和带符号整数的加减运算，以及各种逻辑运算，如与、或、非和异或。理解这些基础概念和电路设计对于理解和开发计算机硬件及软件系统至关重要。