MATLAB实现m序列生成算法

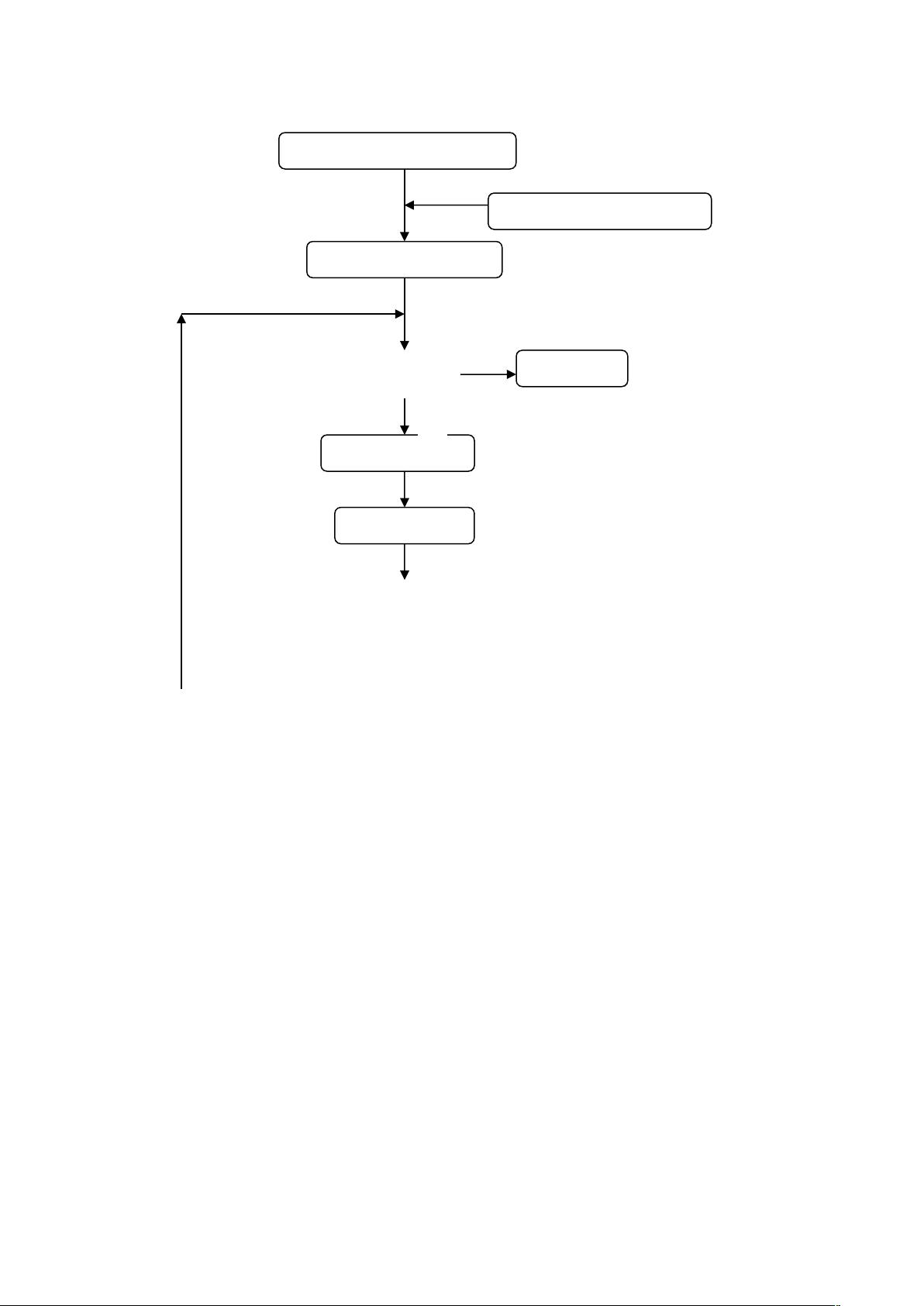
"基于Matlab产生m序列" 在通信领域，m序列是一种重要的伪随机序列，因其优秀的统计特性，如接近白噪声的自相关性和低的互相关性，被广泛应用于扩频通信、同步、加密以及测试信号等领域。m序列是由n级非线性移位寄存器产生的，其周期为2^n，其中n是移位寄存器的级数。这些序列的生成主要依赖于特定的本原多项式，通过这个多项式，可以确定移位寄存器的连接方式。 设计一个m序列通常包括以下几个步骤： 1. **特征多项式确定**：首先需要选择一个本原多项式，它是生成m序列的基础。本原多项式是一个次数大于1的二进制多项式，且在有限域GF(2)中没有除了1之外的根。这样的多项式保证了移位寄存器能生成最长可能的无零串。 2. **本原多项式的确定**：本原多项式的选择至关重要，因为不同的本原多项式会产生不同性质的m序列。一个多项式是否为本原可以通过检查其在有限域内的因子来判断。 3. **m序列的发生**：通过设计移位寄存器结构，根据本原多项式来确定寄存器之间的逻辑关系，如异或门连接。初始状态设定后，每个时钟周期，寄存器的内容会按照设定的规则进行移位，从而产生m序列。 在Matlab环境中，生成m序列的程序通常涉及以下步骤： - 定义本原多项式，这可以是一个二进制向量或十进制表示。 - 创建移位寄存器结构，可以使用向量或矩阵来模拟寄存器。 - 设定初始状态，即寄存器的初始值。 - 编写移位和逻辑运算的循环，模拟移位寄存器的工作过程，产生序列。 - 分析生成的序列，检查其自相关性和互相关性，验证其伪随机性。 在给定的设计任务中，要求使用特定的本原多项式和移位寄存器结构生成m序列。设计者需要编写Matlab代码，通过图示的移位寄存器结构来实现序列的生成。程序运行后，会得到一个m序列，然后对其相关性进行分析，包括自相关函数和互相关函数的计算，以评估其作为伪随机序列的性能。 最后，通过对m序列的特性分析和实际生成的序列进行仿真，可以得出结论，分析序列的适用性，并可能探讨其在跳频通信中的应用。通过这种方式，我们可以理解m序列的生成原理，提高对伪随机序列设计和应用的理解。