一阶非线性系统分析：平衡状态与相轨迹

"本资源包含了自动控制原理课程的第七章习题及解答，主要讨论了非线性系统的一阶和高阶特性和稳定性分析。" 在自动控制原理中，第七章通常涉及非线性系统和稳定性理论。在这个章节中，有两个重要的知识点： 1. **一阶非线性系统的平衡状态和稳定性分析**： - 在问题7-1中，给出了一阶非线性系统的微分方程：\( \frac{dx}{dt} = 3x^2 - x \)。通过设定\( \frac{dx}{dt} = 0 \)，我们可以找到系统的平衡状态，即\( x_e \)。在这个例子中，存在两个平衡状态：\( x_e = -1 \) 和 \( x_e = 1 \)。 - 对于每个平衡状态，我们可以通过线性化系统微分方程来分析稳定性。对于 \( x_e = -1 \)，线性化后的系统是稳定的，因为其对应的特征值为负。而对 \( x_e = 1 \)，特征值为正，表示这是一个不稳定的平衡状态。 - 相轨迹图显示了系统动态行为。当输入 \( x(0) < 1 \)，系统会收敛到稳定的平衡状态 \( x_e = -1 \)；当 \( x(0) > 1 \)，系统发散；当 \( x(0) = 1 \)，系统行为未定义。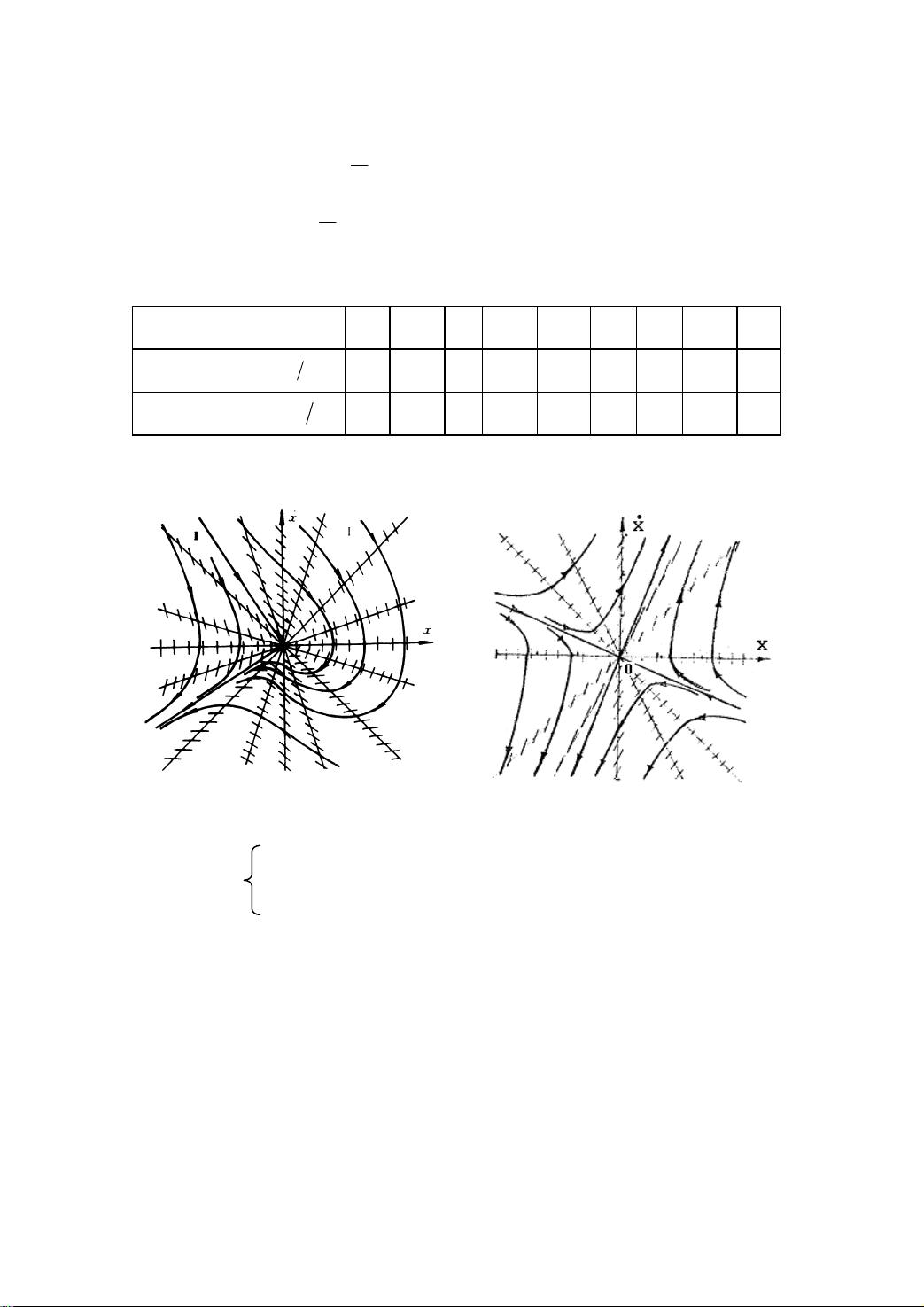 2. **非线性系统的奇点和相轨迹**： - 在问题7-2中，给出了三个不同形式的非线性微分方程。奇点是使非线性项消失的点，对应于系统的特定行为或状态。在这些方程中，我们需要解出 \( f(x) = 0 \) 来找到奇点。 - 对于（1），我们得到一个奇点 \( x_e = 0 \)。对其进行线性化并求解特征方程，可以发现该点是一个不稳定的焦点。 - 对于（2）和（3），没有具体的解过程给出，但一般步骤是同样解出 \( f(x) = 0 \) 来找到奇点，然后进行线性化和稳定性分析。 这个章节的学习要求学生理解非线性系统的行为，掌握如何通过线性化方法分析平衡状态的稳定性，并能绘制相轨迹图来可视化系统动态。这在控制系统设计、分析和优化中是非常基础且重要的技能。