小波变换：三角形图像融合与MATLAB实现

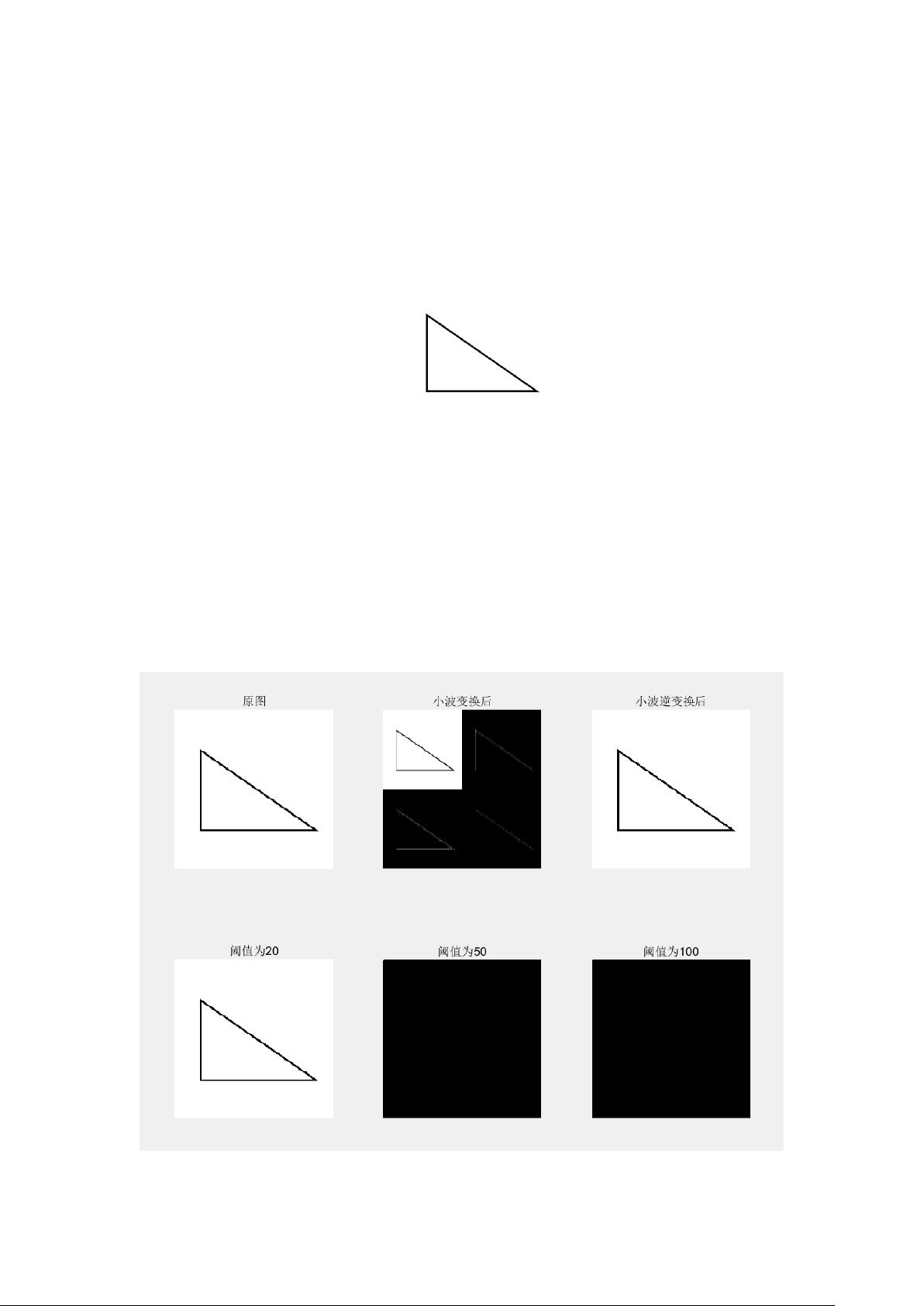
本篇文档是关于小波分析在图像融合中的应用，通过Matlab编程实现对一幅256x256像素的直角三角形BMP图像的处理。首先，作者使用绘图软件创建了这个图像，并将其转换为八位的黑白BMP格式，方便后续编程操作。 小波分析在这个过程中起到了关键作用，它是一种多尺度、方向敏感的信号分析方法。作者选择了一个20（n1）、50（n2）和100（n3）的阈值来分别展示小波变换的效果。程序流程包括： 1. **读取图像**：使用`imread`函数加载名为'Triangle256.bmp'的图像到变量x1，作为原始数据。 2. **小波基定义**：创建一个二维矩阵w1，用于计算小波变换。在循环中，根据模数为偶数和奇数，分配不同的权重值，形成一维离散小波基。 3. **小波变换**：将x1转换为双精度浮点数，然后用w1进行卷积，得到小波变换结果y3。 4. **可视化小波变换**：分别展示了小波变换后的图像，观察到原图像的特征被不同程度地去除，如直角三角形的水平线和竖直线。 5. **阈值处理**：对小波系数矩阵y3进行阈值处理，根据n1和n2设置不同的阈值，将低于阈值的系数置零，这有助于保留重要的图像细节。 6. **小波逆变换**：使用`inv(w1)`求得小波基的逆，然后对处理过的y3进行卷积，得到阈值处理后的小波逆变换结果x4和x5。 7. **显示结果**：最后，将阈值处理后的图像显示出来，分别标上了'阈值为20'和'阈值为50'的标题，以对比不同阈值下图像融合的效果。 这个作业展示了小波分析如何用于图像处理，通过小波变换提取图像特征，再通过阈值处理和逆变换恢复图像信息，实现不同图像的融合。这种方法在数字信号处理和图像处理领域有着广泛的应用，尤其是在图像压缩、去噪和特征提取等方面。通过编写Matlab代码，学生可以深入理解小波分析的核心原理以及其实现过程。