图的遍历:深度优先搜索与广度优先搜索算法解析
需积分: 13 150 浏览量
更新于2024-09-13
收藏 99KB DOC 举报
"图的两种遍历算法:深度优先搜索(DFS)和广度优先搜索(BFS)是图论中的核心算法,广泛应用于解决各种问题,如判断图的连通性、拓扑排序和寻找最短路径等。这些算法在计算机科学中具有重要地位,特别是在数据结构和算法设计中。
深度优先搜索是一种递归策略,它从图中的某个顶点开始,尽可能深地探索图的分支,直到到达叶子节点或所有相邻节点都被访问。在遍历过程中,使用一个辅助数组`visited`来标记已经访问过的顶点,避免重复访问。对于无向图和有向图,DFS的基本步骤如下:
1. 选择一个未访问的顶点作为起始点。
2. 访问该顶点,并将其标记为已访问。
3. 对于每个未访问的邻接点,递归地执行DFS。
4. 当所有邻接点都被访问后,返回上一层并继续处理其他未访问的邻接点。
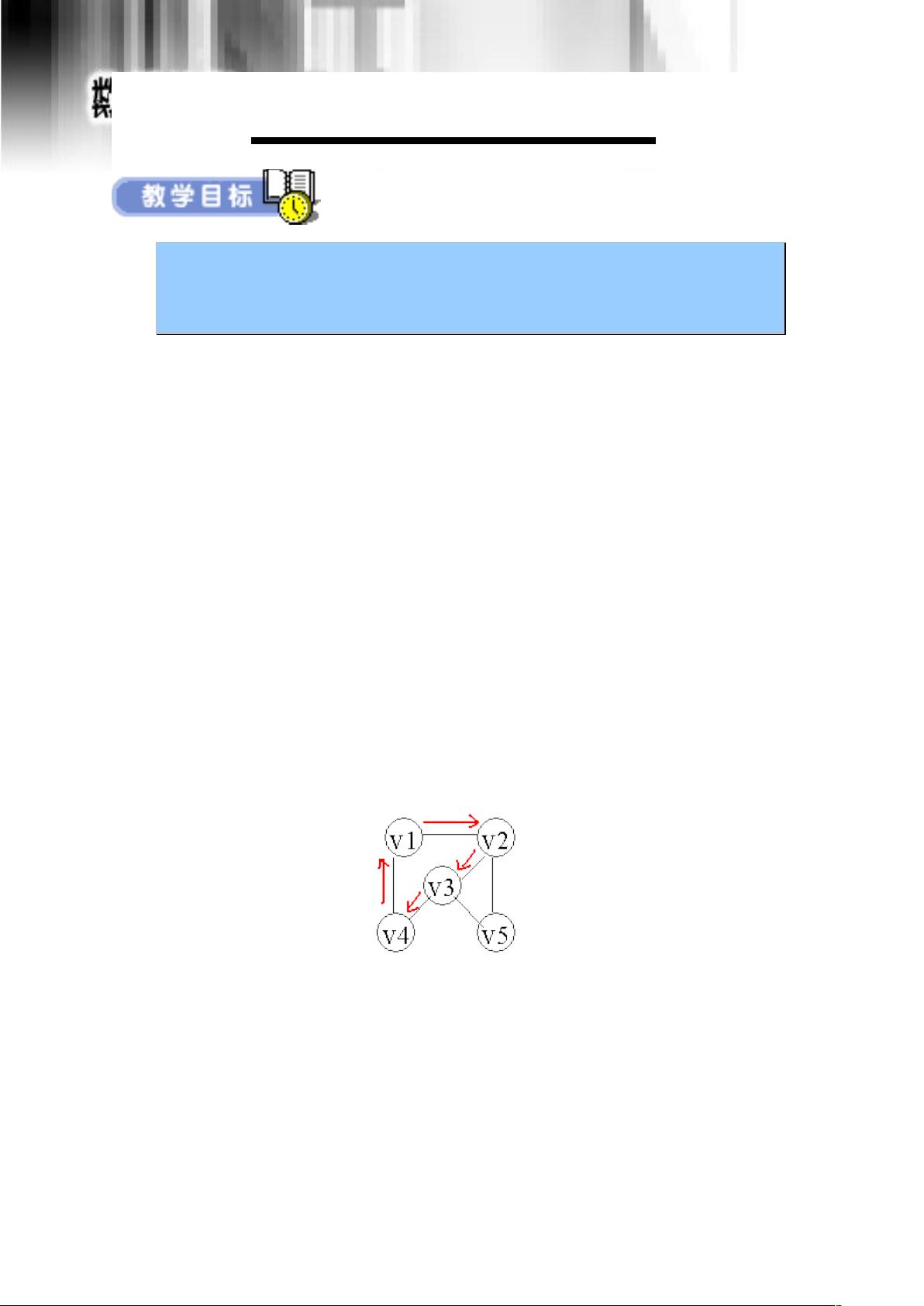
以图5-3-1中的G为例,若以v0为起点,DFS会按照v0 -> v1 -> v3 -> v7 -> v4的顺序进行,然后回溯至v3,再回溯至v1,之后访问v2,继续搜索v2的邻接点。
相比之下,广度优先搜索是一种层次遍历策略,它从起始顶点开始,逐层访问所有相邻节点,然后再进入下一层。BFS使用队列来存储待访问的顶点,确保先访问距离起点近的节点。BFS的主要步骤包括:
1. 将起始顶点放入队列,并标记为已访问。
2. 取出队首元素,访问该顶点。
3. 将该顶点的所有未访问邻接点加入队列。
4. 重复上述过程,直到队列为空,表示所有可达顶点都被访问过。
同样以图5-3-1的G为例,BFS将按照v0 -> v1 -> v2 -> v3 -> v4 -> v7的顺序进行,确保了所有邻接点在同一层被访问。
在解决实际问题时,DFS和BFS各有优缺点。DFS常用于发现图中的环、找出最深的路径或求解回溯问题,而BFS则适用于找到最短路径、求解最小生成树等问题。理解并灵活运用这两种遍历算法,对于理解和解决问题具有重大意义。
教学中,掌握DFS和BFS的关键在于理解它们的搜索策略和状态转移,以及如何利用它们解决实际问题。理解这两个算法的工作原理,能够帮助学生更好地应对复杂的数据结构问题,并为高级算法的学习打下坚实基础。"
2018-05-31 上传
2022-05-29 上传
2021-10-10 上传
2021-10-10 上传
2015-05-12 上传
2022-05-06 上传
2022-07-13 上传
datangtime
- 粉丝: 0
- 资源: 11
最新资源
- 高清艺术文字图标资源,PNG和ICO格式免费下载
- mui框架HTML5应用界面组件使用示例教程
- Vue.js开发利器:chrome-vue-devtools插件解析
- 掌握ElectronBrowserJS:打造跨平台电子应用
- 前端导师教程:构建与部署社交证明页面
- Java多线程与线程安全在断点续传中的实现
- 免Root一键卸载安卓预装应用教程
- 易语言实现高级表格滚动条完美控制技巧
- 超声波测距尺的源码实现
- 数据可视化与交互:构建易用的数据界面
- 实现Discourse外聘回复自动标记的简易插件
- 链表的头插法与尾插法实现及长度计算
- Playwright与Typescript及Mocha集成:自动化UI测试实践指南
- 128x128像素线性工具图标下载集合
- 易语言安装包程序增强版:智能导入与重复库过滤
- 利用AJAX与Spotify API在Google地图中探索世界音乐排行榜