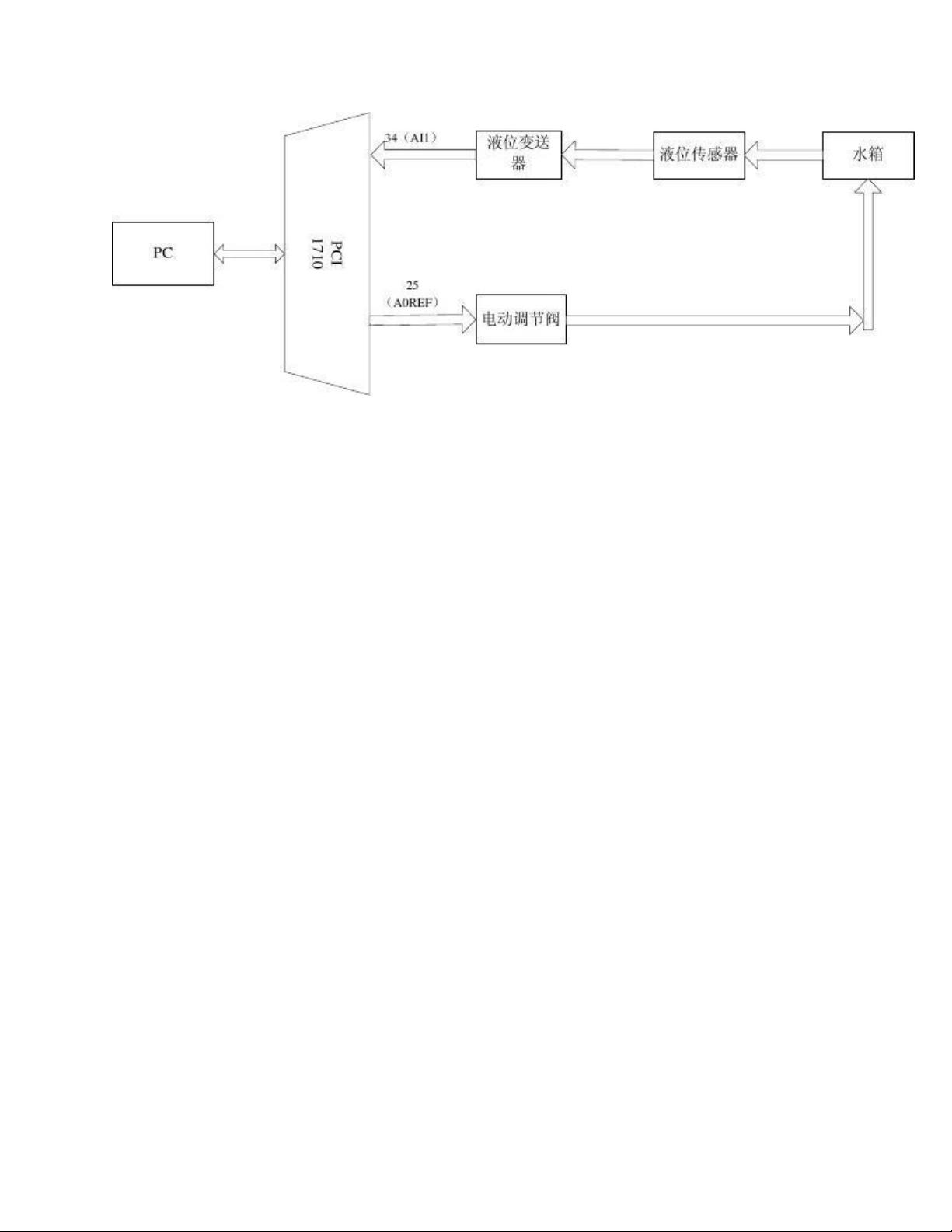
水箱水位模糊控制系统MATLAB实现与仿真
190 浏览量
更新于2024-01-05
5
收藏 2.93MB DOC 举报
智能控制及MATLAB实现-水箱液位模糊控制仿真设计(完整版)资料介绍了一种水箱水位模糊控制系统的设计方法,并借助MATLAB软件进行了实现和仿真。该设计可以通过模糊逻辑工具箱建立一个基于模糊推理系统的控制模型,以实现对水箱液位的精确控制。
在MATLAB中,通过输入sltank命令可以打开模型窗口,显示了水箱液位的仿真图。然后,通过输入fuzzy命令,可以打开模糊逻辑工具箱的图形用户界面窗口,创建一个Mamdani模糊推理系统。该系统由两个输入变量和一个输出变量组成,分别为水位误差、误差变化和阀门开关速度。
为了设计模糊化模块,首先需要定义水位误差和误差变化的论域范围。在本设计中,水位误差的论域范围为[2.95, 3.05],而误差变化的论域范围为[-0.2, 0.2]。而且,在该模糊化模块中,水位误差被划分为7个模糊集,包括NB、NM、NS、ZE、PS、PM、PB;同时,误差变化也被划分为5个模糊集。图3中给出了输入变量的划分情况。
对于每个模糊集,都可以设置其隶属度函数,本设计中,所有模糊集的隶属度函数均为高斯函数。根据给定的参数[0.01 2.95]、[0.01 2.97],[0.01 2.99]、[0.01 3]、[0.01 3.01]、[0.01 3.03]、[0.01 3.05],可以得到每个模糊集的隶属度函数。
在模糊推理系统中,通过设定一组模糊规则,可以将输入变量的模糊值映射到输出变量的模糊值。本设计中,给出了一些模糊规则的示例,来说明如何进行模糊推理。根据这些规则,可以得到输出变量阀门开关速度的模糊集。
最后,通过将输入变量的模糊值和模糊规则结合,可以得到输出变量的具体值。该设计中,通过设定模糊集合的中心(也称为模糊中心)来确定输出变量的模糊值。根据模糊集合中心的不同选择,可以得到不同的输出变量值,在MATLAB中,可以使用defuzz命令来进行模糊化处理。
综上所述,通过智能控制及MATLAB实现-水箱液位模糊控制仿真设计(完整版)资料,我们可以了解到如何使用MATLAB软件进行水箱水位模糊控制系统的设计和仿真。该设计方法可以通过模糊逻辑工具箱创建一个Mamdani模糊推理系统,并通过定义模糊化模块、设置隶属度函数、设计模糊规则等步骤来实现对水箱液位的精确控制。
2009-03-11 上传
2021-12-08 上传
2021-09-24 上传
2023-07-05 上传
2024-03-25 上传
2021-10-10 上传
2022-05-10 上传