PCA、ICA与LDA:图像表示方法的对比分析
"PCA,ICA和LDA是三种常见的降维和表示学习方法,它们在处理高维数据时具有重要作用。本文将对这三种方法进行详细介绍并进行比较。PCA(主成分分析)是一种线性变换技术,通过训练数据来寻找低维子空间。ICA(独立成分分析)的目标是找到数据源的非高斯分布,而LDA(线性判别分析)则更关注分类,旨在找到最大化类别间差异和最小化类别内差异的投影方向。"
PCA(主成分分析):
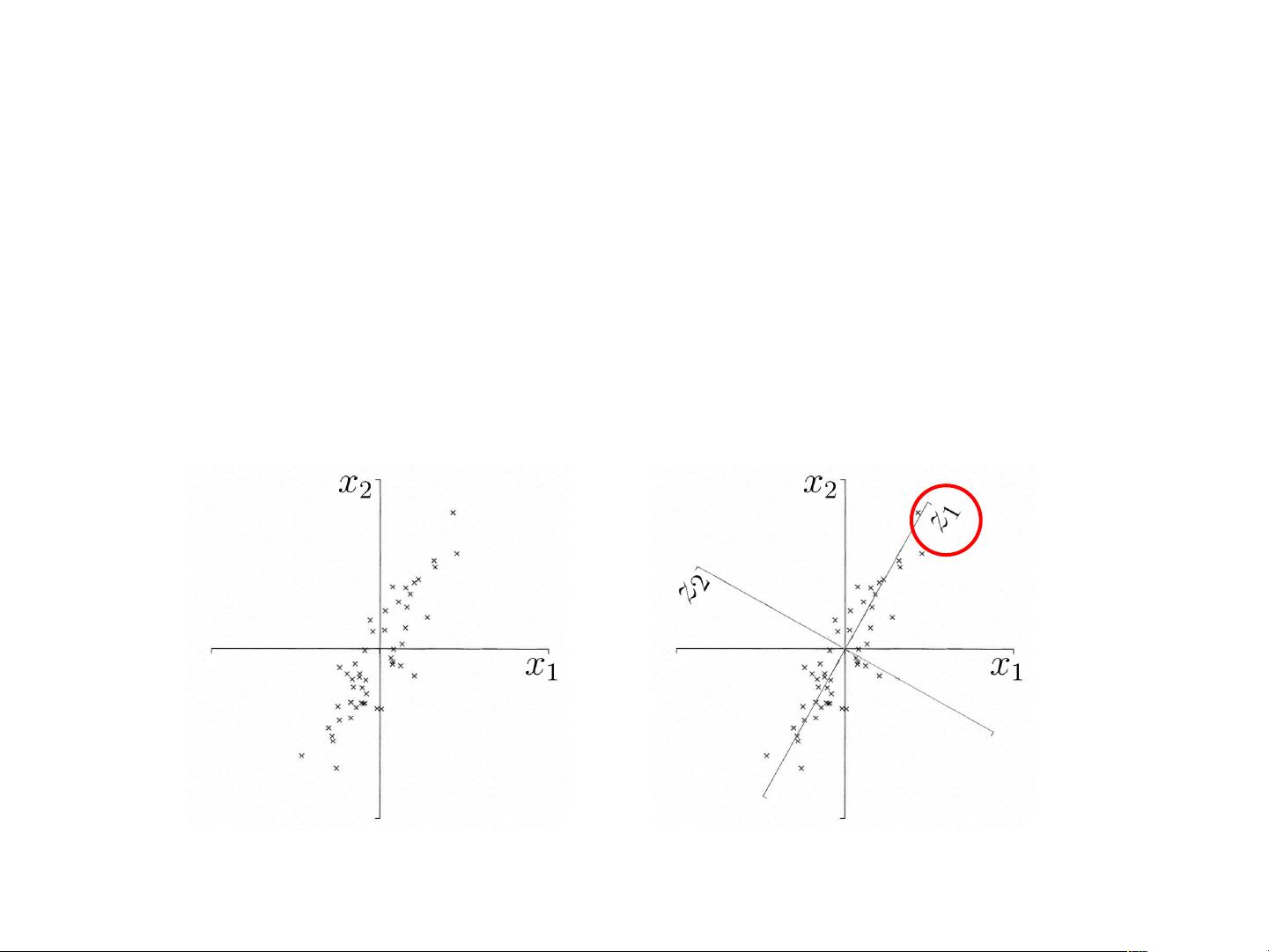
PCA的主要目标是减少数据的维度,同时保留尽可能多的信息。它通过将原始高维数据转换到一个新的坐标系,使得新坐标系的轴是原始数据的主成分,这些主成分是按方差降序排列的。这样,我们可以丢弃包含较少信息的高维成分,从而降低数据的复杂性。PCA的关键步骤包括数据中心化、计算协方差矩阵、求解特征值和特征向量,以及选择最重要的几个主成分构建低维空间。
ICA(独立成分分析):
ICA是一种无监督学习方法,旨在分离混合信号源,假设这些信号源是相互独立且非高斯分布的。ICA不同于PCA,它不仅仅关注数据的方差,而是寻找数据的潜在独立成分。ICA算法通常包括预处理、估计源模型、解混矩阵计算和恢复独立成分等步骤。ICA常用于盲源分离问题,如音频信号分离或脑电图(EEG)分析。
LDA(线性判别分析):
LDA是一种有监督的学习方法,主要用于分类问题。LDA通过最大化类间距离(互斥性)和最小化类内距离(凝聚性)来找到最佳投影方向。LDA的目标是找到一个低维空间,使得在该空间中的类间距离最大,类内距离最小。LDA适用于预处理特征用于分类任务,例如人脸识别或文本分类。
比较:
PCA是无监督的,主要关注数据的统计特性,如方差,而ICA和LDA则考虑了数据的潜在结构和分类信息。ICA适合于寻找非高斯分布的独立源,而LDA更适合于分类任务,特别是在有标签数据的情况下。在实际应用中,选择哪种方法取决于具体任务的需求,如数据的性质、是否有标签信息以及降维目的等。
总结:
PCA,ICA和LDA都是处理高维数据的有效工具,但它们各有侧重。PCA是基于统计特性的降维,ICA关注于独立信号源的恢复,而LDA则聚焦于分类性能的提升。理解这些方法的原理和适用场景,对于选择合适的数据表示和降维策略至关重要。在实际工作中,这些方法可以单独使用,也可以结合使用以达到更好的效果。
1306 浏览量
337 浏览量
220 浏览量
110 浏览量
276 浏览量
2021-09-30 上传
243 浏览量
点击了解资源详情
jiexing007
- 粉丝: 0
- 资源: 3
最新资源
- 图书管理备案系统.rar
- the_computer_vision_app:一款可在网络上执行常见的计算机视觉任务的应用程序
- java笔试题算法-C5:用于C#/.NET的C5泛型集合库
- comment2votes:seq2seq架构,用于预测reddit评论的投票
- andyseoDB
- 家居城促销顾客须知(转盘上摇奖的注意事项)
- 永宏PLC编成软件 适合FBE FBS B1Z等型号.rar
- file-system-access:公开用户设备上的文件系统,以便Web应用程序可以与用户的本机应用程序进行互操作
- jstl-tld.zip
- Ikasumi-crx插件
- 超可爱卡通动物图标下载
- 任务一-使用监督的机器学习预测:根据编号预测学生的百分比。 学习时间
- CSE212_DataStructures_Guide
- 初级java笔试题-awesome-php-resources:精选的很棒的php列表
- ךופה לע ךופה - הפוך על הפוך-crx插件
- 作业六