数学模型：插值与拟合方法解析

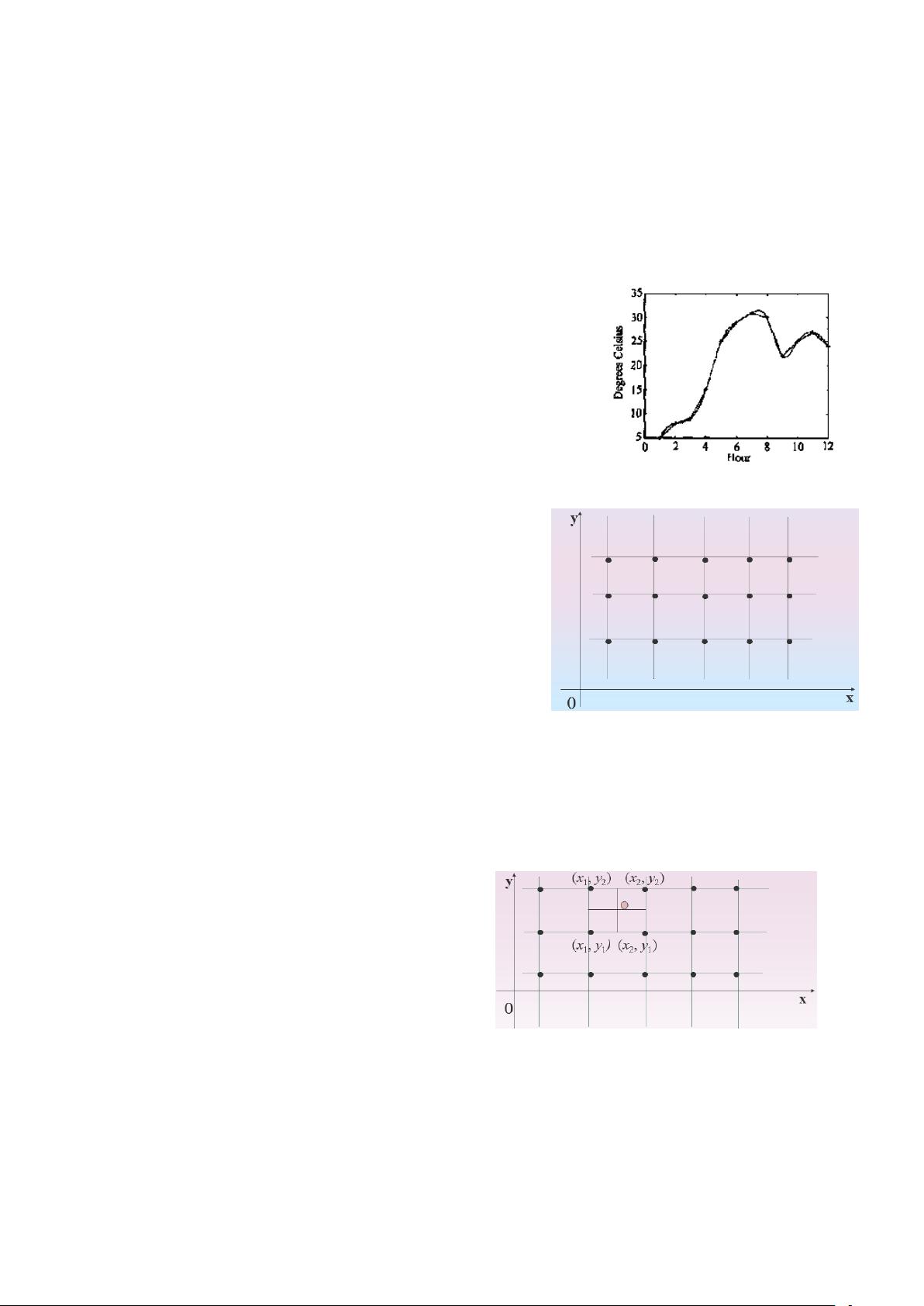
"插值与拟合建模是数学模型算法中的重要组成部分，主要涉及如何构建函数来逼近给定数据点。这一讲主要讲解了一维插值和二维插值的方法，以及在实际问题中的应用。" 在数学建模中，插值是一种基本技术，用于寻找一个函数，使得该函数在特定的离散点上与给定的数据值相匹配。一维插值问题通常涉及到在已知一些离散点的情况下，找到一个合适的函数，使得这个函数在每个点上的值都与给定的数据一致。 1. 一维插值方法包括： - Lagrange插值：利用Lagrange基函数构造一个n次多项式，该多项式通过所有n个给定点。Lagrange插值公式为 ，其中 是第i个Lagrange基函数， 是第i个插值点的函数值。 - 特殊情形：线性插值（两点插值）和抛物线插值（三点插值）。例如，线性插值公式为 ，抛物线插值公式为 。 实际应用示例：在温度监测数据中，利用线性和抛物线插值来估算不同时间点的温度。 2. 分段线性插值：在某些情况下，可能需要使用多个线性段连接各个点，以形成一个更平滑的插值曲线。例如，分段线性插值函数形式为 ，其中 为不同的线性插值段。 3. Matlab中的一维插值：可以使用`interp1`函数进行一维插值计算，如例2所示，通过给定的时间间隔和温度数据，使用`spline`插值方法得到更精细的时间点上的温度估计。 二维插值则更为复杂，因为它涉及到在平面或更高维度空间中处理数据点。 1. 网格节点插值法：对于二维情况，可以构建一个通过所有给定节点的二元函数，然后使用该函数进行插值。常见的方法包括： - 最邻近点插值：简单地采用最近的数据点的值作为插值结果，但可能存在不连续性问题。 - 分片线性插值：将数据点视为矩形的顶点，通过构建两片线性函数覆盖整个矩形区域，每片函数满足两个边上的插值条件。 这些插值方法在数据可视化、图像处理、数值分析等领域有着广泛的应用。例如，对于非均匀分布的测量数据，插值可以用来填充缺失值或提高数据分辨率。拟合则是另一个相关的概念，它不仅要求函数通过所有点，而且还要最小化误差，以找到最佳拟合模型。拟合方法如最小二乘法和多项式回归等，是数据分析和预测的重要工具。 总结起来，插值与拟合建模是数学模型算法中不可或缺的部分，它们提供了处理离散数据的有效手段，帮助我们理解和预测复杂的现实世界现象。通过学习和熟练掌握这些方法，可以提升数据分析和建模的能力。