数字信号处理与软件无线电技术

需积分: 9 176 浏览量更新于2024-07-31 收藏 5.85MB PDF 举报

"深入理解数字信号处理（DSP）与软件无线电设计" 在当今的科技领域，数字信号处理（DSP）扮演着至关重要的角色。DSP是过去一百年中的重大技术创新，不仅在无线电通信中得到广泛应用，还渗透到了石油和其他化石燃料的勘探、高清晰度电视（HDTV）、压缩光盘（CD）录制等多个生活领域。其普及性源于几个关键优点：首先，DSP滤波器无需调谐，可以精确地从一个单元复制到另一个单元，保证了滤波效果的一致性；其次，由于工作在数字环境中，温度变化对系统性能的影响几乎可以忽略不计；最后，DSP提供了极高的灵活性，通用的DSP硬件通过编程可以执行多种不同的功能，往往能替代专门的硬件模块，降低了系统的复杂性和成本。 DSP的基础原理在于快速测量模拟信号，将这些测量值转化为数字序列进行处理，然后将处理后的数字序列再转换回模拟信号。这一过程通常包括以下几个步骤： 1. **采样（Sampling）**：当模拟信号的频率远低于采样频率时（如图16.1所示），可以确保无失真地捕获信号。奈奎斯特定理是指导采样过程的关键理论，它规定了最小采样频率应为信号最高频率的两倍，以避免混叠现象。 2. **量化（Quantization）**：将采样得到的连续幅度转换成离散的数字值。这个过程可能会引入量化噪声，但可以通过提高量化位数来降低这种噪声。 3. **编码（Encoding）**：将量化后的值用二进制形式表示，以便于数字处理。 4. **数字信号处理（DSP）**：利用各种算法，如滤波、增益控制、谱分析等对数字序列进行操作。这些算法可以在软件中实现，使得系统具有高度可配置性和可升级性。 5. **解码（Decoding）**：处理后的数字信号需要转换回模拟信号，这通常通过数模转换器（DAC）完成。 6. **重构（Reconstruction）**：最后，通过低通滤波器消除采样过程中产生的图像信号，恢复原始模拟信号。软件无线电（Software Defined Radio, SDR）是DSP在无线通信领域的应用典范。SDR的核心思想是将传统的硬件功能，如调谐、解调和信号处理等，尽可能地转移到软件中实现。这样可以灵活地适应不同的通信标准，只需更新软件即可调整电台的工作模式。此外，SDR还可以利用现代计算机的高速计算能力，实现更复杂的信号处理算法，如多载波调制和认知无线电技术，提高通信系统的效率和适应性。 DSP与软件无线电设计结合了数字技术的优势，实现了对信号处理的高度控制和灵活性，推动了通信、娱乐、科研等诸多领域的技术进步。随着技术的不断发展，我们可以预见到更多创新的应用将基于DSP和SDR技术得以实现。

16.8 Chapter 16

the signal path.

The direct form of Eq 8 may be factored

into 2-pole sections and implemented in

cascaded form. The output of each section

serves as the input to the next. See Fig 16.7.

This configuration requires a few more

multiplications than the direct form, but suf-

fers less from instability problems that may

plague IIR filters. Since feedback is being

used, IIR filters are not necessarily uncon-

ditionally stable. They also tend to be prone

to limit cycles, low-level oscillations that

arise near the lower end of the dynamic

range. For these and other reasons, data and

coefficient storage should be cleared or set

to zero before processing begins.

A Simple Digital Notch Filter

Along with common LPFs, HPFs and

BPFs, radio designers are interested in one

other type of filter, the notch. While most

filter-design software can generate notch

filters using FIR methods discussed above,

Widrow and Stearns have described an un-

usual type in which the number of taps is

minimized. In fact, they were able to prove

that only two taps are needed for each fre-

quency to be notched. This is great, since it

reduces computation to almost nil. We will

take a look at it here and touch briefly on

some of the theory of adaptive signal pro-

cessing, treated in depth later.

The situation is this: We want to copy a

broadband signal, such as an SSB phone

signal, and suddenly a dreadful carrier

appears in the passband. Our notch filter

will remove it and we will have complete

control over the notch width, as well as a

notch depth limited only by the bit resolu-

tion of our system. Dr Widrow found that

one can build a filtering system that mini-

mizes repetitive signal energy by altering

the filter coefficients “on the fly” using a

certain algorithm. Known as the least-

mean-squares (LMS) method, it describes

a way to adjust filter coefficients over time

to remove undesired, steady tones in the

input. A complex reference signal is used

at the exact frequency of the offending

tone. The algorithm then forms a BPF cen-

tered at the tone frequency whose output

is subtracted from the input to create the

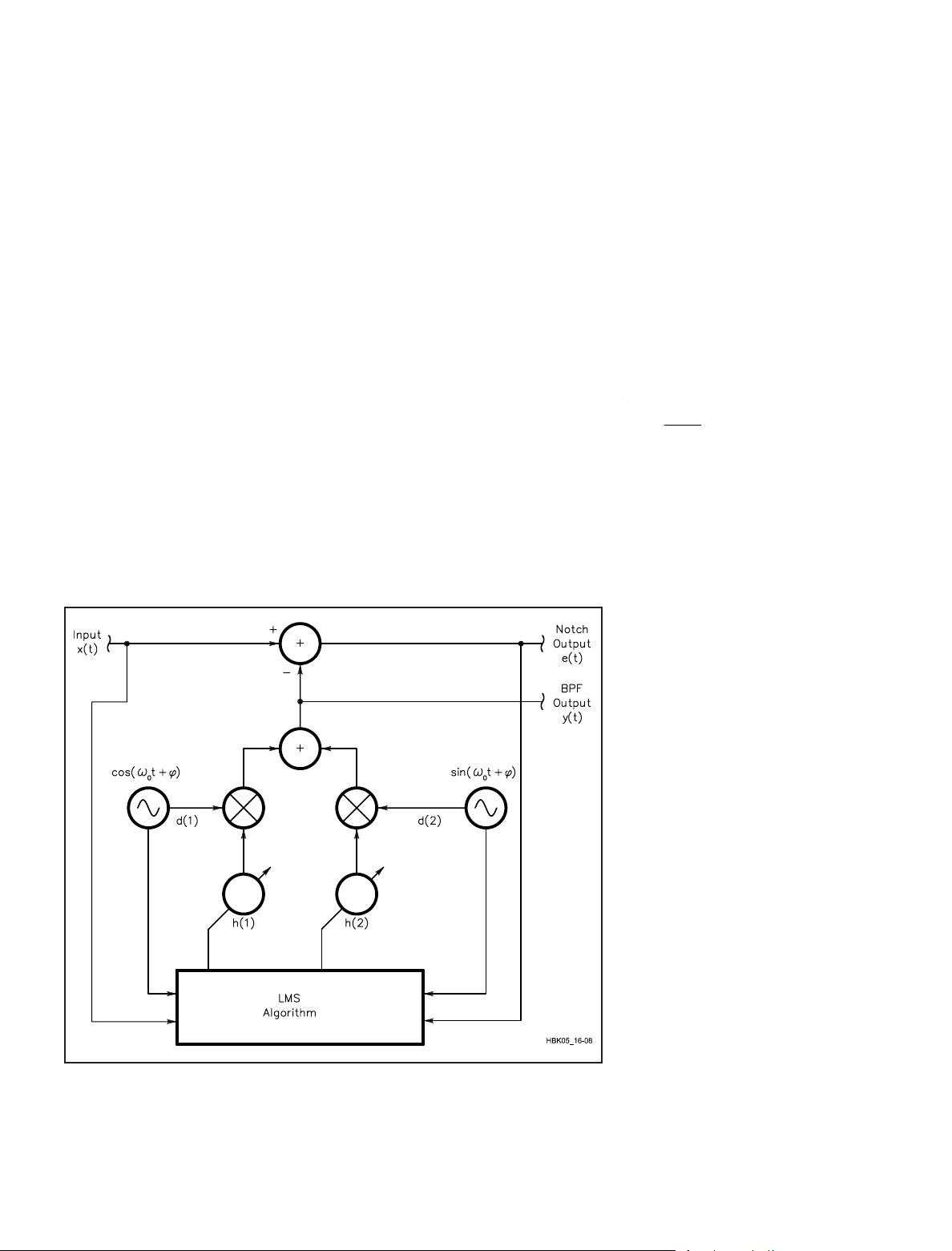
notch. The block diagram of a two-tap

system is shown in Fig 16.8.

The broadband input is called x(t). The

reference input consists of two signals, cos

(ω

t) and sin (ω

t). These signals feed

multipliers having coefficients h(1) and

h(2), which in turn feed an accumulator

just as in a normal FIR filter. This is the

BPF output; it is subtracted from the input

to form the notch output, e(t). Note that

the BPF output is also available at no ad-

ditional overhead. While the initial values

of the coefficients are unimportant to the

steady state, the procedure for updating

them with the LMS algorithm is:

)2(μe(t)x2)2(h)2(h

)1(μe(t)x2)1(h)1(h

tt1t

(9)

where 0 < μ < 1. Analysis shows that as the

reference inputs are sinusoidal, the system

is linear and time-invariant for output e(t),

although the coefficient values do not nec-

essarily approach any fixed value. The 3-dB

BW of the notch is:

rad/s

μA2

(10)

The Q of the filter may be readily com-

puted. Thus, we have control over the BW

by varying the factor μ and the amplitude of

the reference signal. The depth of the null is,

in general, superior to that of a fixed filter

because the algorithm tracks the correct

phase relationship for ideal cancellation,

even if the reference frequency is changing

slowly with the offending tone. Each addi-

tional tone to be notched demands two addi-

tional taps in the filter. Noise in the input

may cause us to have to add more taps to

maintain sufficient accuracy. Additional

detail of adaptive signal processing will be

found below and in material shown in the

Bibliography.

Lattice and Other Structures

While many filter-design software

packages do not have the capability to

work with them, lattice structures and

other types of digital filters have seen use,

especially in adaptive signal processing.

Crystal and mechanical lattice filters are

common elements of many transceivers.

A digital lattice or ladder filter is a lot like

its analog brother. The design of digital

lattice filters is similar as well. Digital

lattice filters may be either FIR or IIR.

Also note that from the IIR cascade form

above, we can derive a parallel form that

may be computationally beneficial in

some cases. The design of this kind of fil-

ter is a very complicated session in partial

fraction expansion. Widrow and Stearns

provide more information on these and

other exotic concepts.

Fig 16.8—Block diagram of a two-tap, adaptive notch filter.

ch16.pmd 7/28/2006, 9:27 AM8

DSP and Software Radio Design 16.9

ANALYTIC SIGNALS AND MODULATION

Fig 16.9—Vector representation of a

real cosine wave.

Fig 16.10—Hilbert transformer

producing an analytic signal.

Fig 16.11—Block diagram of a half-complex mixer.

DSP implementations of transceiver

functions, such as modulation and de-

modulation, compel designers to examine

the mathematics behind them. Computers

are good at crunching numbers, but they

do exactly what they are told! If we expect

a DSP system to generate an SSB signal,

for example, we had better know which

calculations to perform and which to

avoid.

Mathematics of Complex Signals

Because DSP makes it easy to build fre-

quency-independent phase shifters—a

fantasy in the analog world—the phasing

or “I/Q” method has dominated other

modulation techniques. Complex signals

are not generally well understood and

quite often form a stumbling block to those

wishing to grasp DSP concepts. The idea

of negative frequency is especially

troublesome. The key to understanding

these concepts lies in the theory of com-

plex numbers. A real signal, such as a co-

sine wave, is normally thought of as a

positive frequency. It can be transmitted

and detected normally; however, we shall

see that such a signal

actually consists of

positive and negative frequencies when

examined in the complex domain.

A real cosine wave embodies the rela-

tion:

x(t) = cos(wt) (11)

where ω = 2πf and t is time. In the complex

domain, the cosine wave is really the sum

of two complex signals:

[]

⎭

⎬

⎫

⎩

⎨

⎧

−

)tsin(j)tcos(

t)sin(j)tcos(

ωω

)t(x

(12)

This signal has both positive and nega-

tive frequency components. The real parts

add and the imaginary parts cancel to make

the equation true. In the complex plane,

where the real part is one axis and the

imaginary part the other, this signal can be

represented as two vectors rotating in op-

posite directions. See Fig 16.9.

While this depiction is beautiful and

elegant to the mathematician, what does it

really mean to you and me? Well, it means

that signals represented in complex form

can have a one-sided spectrum—that is,

only a positive or a negative frequency

component. This is useful as we mix our

signals upward to their final frequency

positions in a modulator.

As our first example, let’s select the task

of taking a real input signal, such as the

audio from a microphone, and converting

it to an SSB signal that can be transmitted.

We obviously have to translate the audio

signal upward in frequency and preserve

its spectral content within the band we

want the transmitted signal to occupy. If

we wish to produce an upper-sideband

(USB) signal, we want the carrier and

lower sideband to be suppressed as much

as possible. Were we able to translate the

spectrum of our cosine wave—with its

symmetrical positive- and negative-fre-

quency components—upward in fre-

quency far enough, we would have two

positive frequencies separated by twice

the original signal’s frequency. For a real

signal, this is exactly what happens when

it is applied to an analog mixer: Both sum

and difference frequencies are generated.

See the Receivers, Transmitters and

Transverters chapter for more detail of

the operation of mixers as multipliers.

To move our sampled audio signal up-

ward in frequency, we must multiply it by

(mix it with) a local oscillator. The local-

oscillator function can be implemented in

DSP software using direct digital synthesis

(DDS) techniques. In this case, though, the

local oscillator must be complex; that is, it

must have two outputs with a 90° phase rela-

tionship between them. This is the same as

saying there must be both a sine and a cosine

output from it. This will enable us to mix

signals having a one-sided spectrum.

When we implement a complex mixer

in DSP, we are multiplying complex num-

bers by complex numbers. Note that the

calculations for the real and imaginary

parts are carried out separately; each part

is treated as if it were a single, real multi-

plication. Two complex numbers a + j b

and c + j d, when multiplied, produce:

(a + j b)(c + j d) = (ac – bd) + j (ad + bc)

(13)

Four real multiplications and two real

additions are required.

Hilbert Transformers and an SSB

Modulator

If we want to create a signal having a

one-sided spectrum from a real input sig-

nal, such as from the microphone, we need

to shift all the frequency components in

ch16.pmd 7/28/2006, 9:27 AM9

剩余43页未读，继续阅读

jitongzhong

粉丝: 0
资源: 1

数字信号处理与软件无线电技术

一个基于DSP的软件无线电的c语言设计实例

通信接收机：DSP、软件无线电和设计 pdg

通信接收机：DSP，软件无线电和设计

单片机与DSP中的基于高性能DSP的软件无线电平台设计

基于高性能DSP的软件无线电平台系统设计

基于FPGA DSP的软件无线电平台的设计.pdf

单片机与DSP中的软件无线电设计中ASIC、FPGA和DSP的选择策略

2021-2022收藏资料基于FPGA DSP的软件无线电通用平台设计.doc

基于DSP的软件无线电接收机研究和实现.doc

基于DSP软件无线电系统的设计与实现.doc

最新资源