图解广度优先搜索(BFS)：寻找最短路径

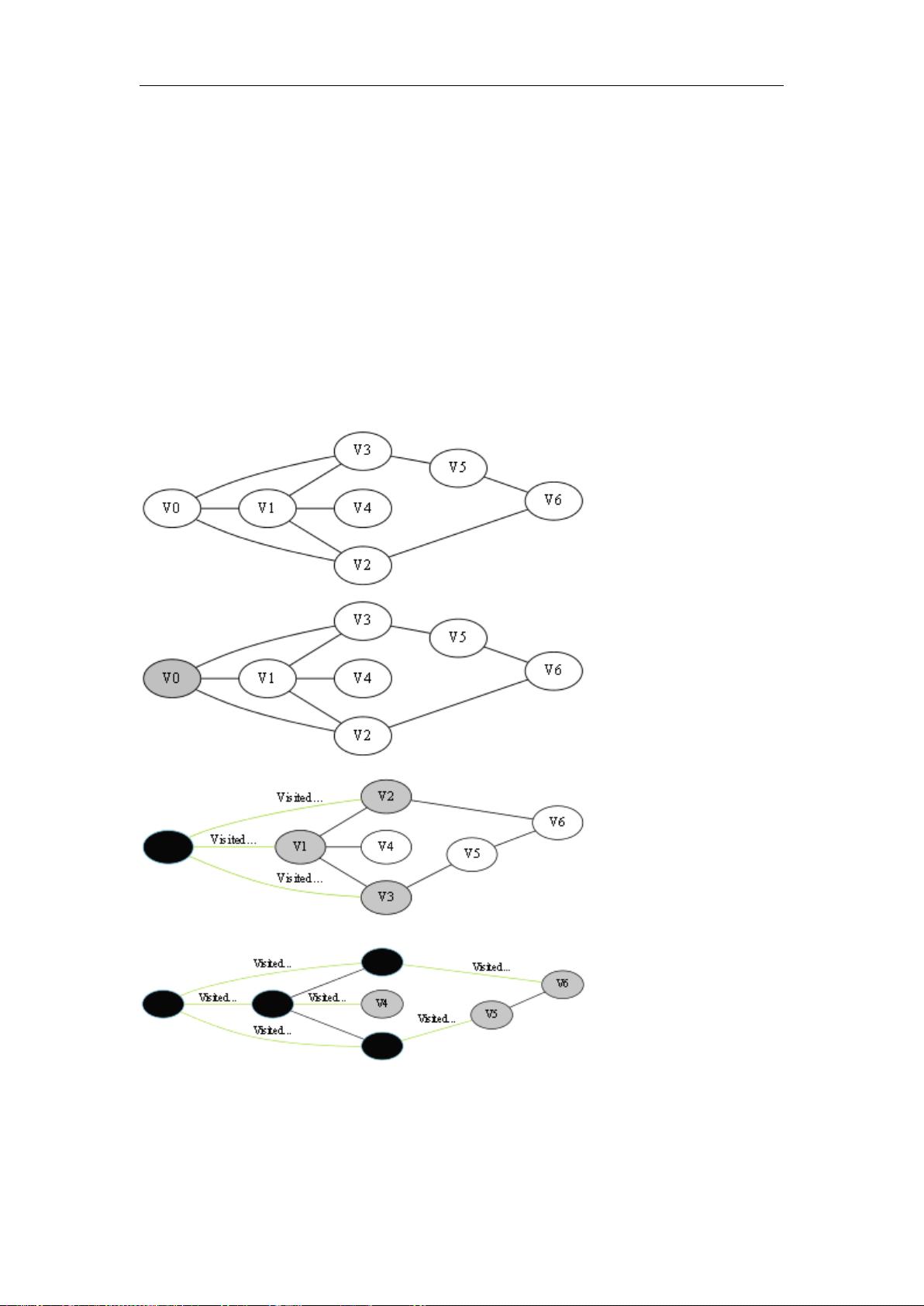
"广度优先搜索(BFS)是一种用于遍历或搜索树或图的算法，它按照从根节点开始，逐层扩展到相邻节点的顺序进行搜索。该算法通常用于寻找最短路径或解决连通性问题。" 在计算机科学中，广度优先搜索（BFS）是一种基础且重要的算法，尤其在处理图论问题时非常有用。BFS的核心思想是逐层探索图的节点，从起点开始，先访问距离起点最近的节点，然后逐渐访问更远的节点。这个过程可以形象地比喻为从中心向外辐射的探索。 1. 前言 BFS通常用于解决“最短路径”问题，比如在无权图中找到两点之间的最短路径。在迷宫问题中，BFS能有效地找到从起点到终点的最短路径。它通过使用队列数据结构来存储待访问的节点，确保了先访问离起点近的节点。 2. 图的概念 图是由顶点（Vertex，用V表示）和边（Edge，用E表示）组成的集合。在连通图中，任意两个顶点之间都存在至少一条路径。无向图表示边没有方向，而有向图则有方向性。图2-1展示了无向连通图的一个实例。 3. 广度优先搜索算法 - 基本思路：BFS算法从给定的起点开始，将起点放入队列。然后，每次从队列头部取出一个节点，检查它是否为目标节点，如果不是，则将其所有未访问过的邻居节点加入队列。重复此过程，直到找到目标节点或队列为空为止。 - 步骤： 1. 初始化一个空队列，将起始节点入队。 2. 当队列非空时，循环执行以下操作： - 取出队首节点，标记为已访问。 - 遍历当前节点的所有邻居，若邻居未被访问过，将其标记并入队。 3. 如果目标节点被标记，结束搜索，返回路径；否则，如果队列为空，说明不存在路径。 4. 应用场景 - 最短路径：BFS适用于寻找无权图中的最短路径，因为它总是先尝试最短的边。 - 连通性判断：BFS可以确定图中两个节点是否连通，如果从一个节点可以到达另一个节点，则它们是连通的。 - 检测环：BFS可以辅助检测有向图中的环，通过记录每个节点的访问顺序，如果遇到已访问过的节点，说明存在环。 5. 实现细节 - 使用队列：BFS的实现通常使用队列作为主要的数据结构，保证了先进先出的特性。 - 记录状态：为了防止重复访问，需要标记已访问过的节点。 - 层次遍历：BFS可以用于层次遍历，即按照节点的层次依次访问，例如在社交网络中找出一个人的所有朋友的朋友。 总结来说，广度优先搜索（BFS）是一种有效的图遍历方法，广泛应用于寻找最短路径、判断连通性以及检测环等问题。理解并掌握BFS算法对于解决各种图论问题至关重要。