"图像矢量化中的正交最小二乘拟合算法-数据仓库与数据挖掘实验报告"
版权申诉
110 浏览量
更新于2024-04-05
收藏 546KB PDF 举报
格化的逆过程相对比较困难。在本实验中,我们将使用正交最小二乘拟合算法来对图像进行矢量化处理。具体来说,我们将首先将图像进行边缘检测,然后通过曲线拟合算法找到最佳拟合曲线,最终将图像转换成矢量形式。
2. 实验设计与要求
实验要求:
(1)选择一个简单的图标作为实验对象,保存成一定分辨率的位图文件。
(2)使用MATLAB编程,读取位图文件,进行边缘检测。
(3)对边缘点集进行正交最小二乘拟合,得到最佳拟合曲线。
(4)将曲线方程输出,并绘制矢量化后的图像。
实验设计:
(1)读取位图文件,将像素点转换成坐标点,进行边缘检测。
(2)利用正交最小二乘拟合算法对边缘点集进行曲线拟合。
(3)输出曲线方程,绘制矢量化后的图像。
(4)对实验结果进行评估,分析矢量化效果。
3. 实验过程与结果
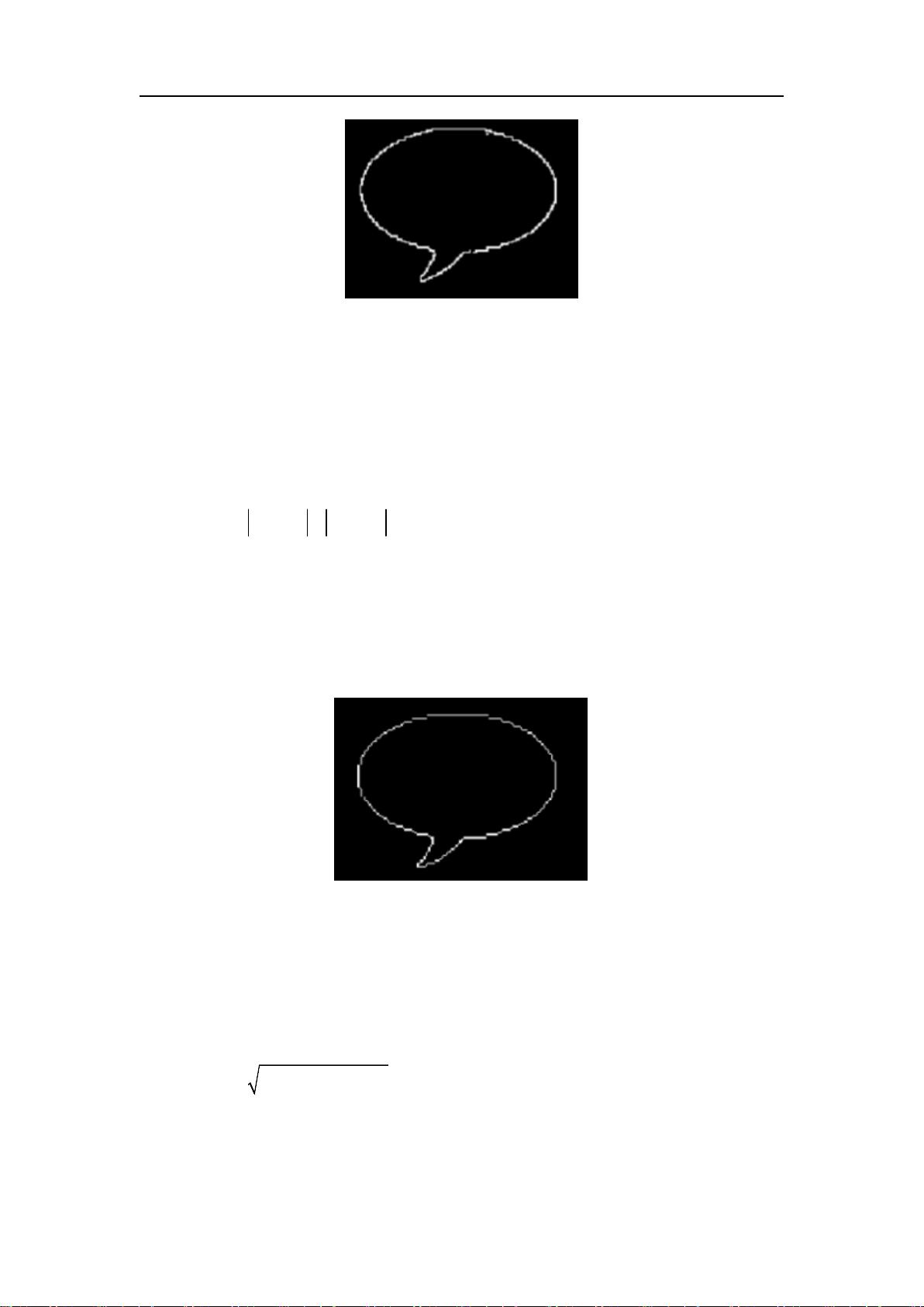
在实验过程中,我们首先选择了一个简单的图标作为实验对象,将其保存成位图文件。然后,我们编写MATLAB程序,读取位图文件,并进行边缘检测。通过Sobel算子等方法,我们成功提取出图像的边缘点集。
接下来,我们使用正交最小二乘拟合算法对边缘点集进行曲线拟合。通过最小化点到曲线的距离,我们得到了最佳拟合曲线的参数,并输出了曲线方程。最终,我们将曲线方程应用到原始图像上,绘制了矢量化后的图像。
实验结果表明,通过正交最小二乘拟合算法,我们成功将图像转换成矢量形式,并且保持了图形的准确性和清晰度。矢量化后的图像可以任意放缩而不失真,适合于工程制图、标志设计等应用场景。
4. 实验总结与展望
本实验基于正交最小二乘拟合算法,实现了图像的矢量化处理。通过边缘检测和曲线拟合,我们成功将图像转换成矢量形式,并保持了图形的精确性。然而,实验中也存在一些问题和不足之处,比如对复杂图像的处理效果可能不尽如人意,需要进一步优化算法和方法。
未来,我们可以考虑结合深度学习等方法,提高图像处理的精度和效率。同时,可以探索更多图像处理技术,拓展实验的应用范围。总的来说,本实验为我们提供了一个深入了解图像处理算法和矢量化技术的机会,对于提升我们的数据仓库与数据挖掘能力具有重要意义。最后,我们希望通过对该实验的深入研究和实践,不断提升自己的编程能力和解决问题的能力。"
点击了解资源详情
793 浏览量
220 浏览量
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
passionSnail
- 粉丝: 470
最新资源
- Delphi7.0构建的图书销售管理系统设计
- 51单片机C语言入门:使用KEIL uVISION2开发
- 掌握XML:实用教程与核心技术
- C# Programming Fundamentals and Applications
- LoadRunner入门:实战测Tomcat表单性能与脚本录制
- 松下KX-FLB753CN一体传真机中文说明书:安全与操作指南
- Java语言入门学习笔记
- 哈工大线性系统理论硕士课程大纲
- DS18B20:一线总线数字温度传感器详解
- 数据库表设计实战指南:主键选择与规范化策略
- Protel DXP中文版入门教程:构建原理图与PCB设计
- 正则表达式完全指南:常见模式与解析
- Linux世界驰骋系列教程全集:系统管理与Shell编程
- 软件工程:走进成熟的学科指南(第4版)
- .NET初学者指南:C#基础教程
- Oracle常用函数详解:从ASCII到RPAD/LPAD