三维有限元分析：复合材料弹性模量预测

"这篇论文是2009年由刘旭东和张劲松发表在《沈阳工程学院学报（自然科学版）》上的，探讨了如何使用有限元法预测三维网络和颗粒增强复合材料的有效弹性模量。他们建立了一个有限元模型来分析SiC三维网络和颗粒增强金属基复合材料的弹性模量与增强体含量之间的关系，发现这种关系是非线性的。在相同的增强体体积分数下，三维网络增强复合材料表现出更高的杨氏模量、体积模量和剪切模量。" 这篇研究论文涉及的知识点包括： 1. **有限元法**：有限元法是一种数值计算方法，常用于解决复杂的工程和物理问题，特别是结构力学问题。在这里，它被用来预测复合材料的弹性模量。 2. **复合材料**：复合材料是由两种或更多不同材料组成的，其中一种材料（基体）被另一种材料（增强体）强化，以改善整体性能。在这项研究中，重点关注的是三维网络和颗粒增强的金属基复合材料。 3. **弹性模量**：弹性模量是材料的固有属性，表示材料抵抗形变的能力。它是材料力学性能的重要指标，包括杨氏模量（沿一个方向的拉伸弹性模量）、体积模量（体积变化时的弹性模量）和剪切模量（剪切变形下的弹性模量）。 4. **增强体含量**：增强体在复合材料中的体积分数直接影响材料的弹性模量。论文指出，弹性模量与增强体的体积分数呈非线性关系，且随含量增加而增加。 5. **三维网络增强**：相对于传统的颗粒增强，三维网络增强提供了更连续的增强路径，从而可能提高复合材料的力学性能。 6. **颗粒增强复合材料**：颗粒增强复合材料是由颗粒状增强体分散在基体材料中形成的，这种增强方式可以提高材料的强度和韧性。 7. **Eshelby等效夹杂理论**：Eshelby理论是预测复合材料弹性模量的经典方法，它假设夹杂（增强体）在基体中是均匀分布的，并可以等效为单一的弹性体。 8. **Mori-Tanaka方法**：这是一种统计平均理论，用于计算多相复合材料的平均弹性常数，考虑了相间的相互作用。 9. **微分介质方法**和**变分原理**：这些是另外两种理论框架，用于预测复合材料的弹性性质，它们基于微分方程或变分原则来求解。 10. **颗粒大小的分布规律**：齐海波等人的工作考虑了颗粒大小分布对预测弹性模量的影响，这种方法可能不适用于三维网络增强复合材料。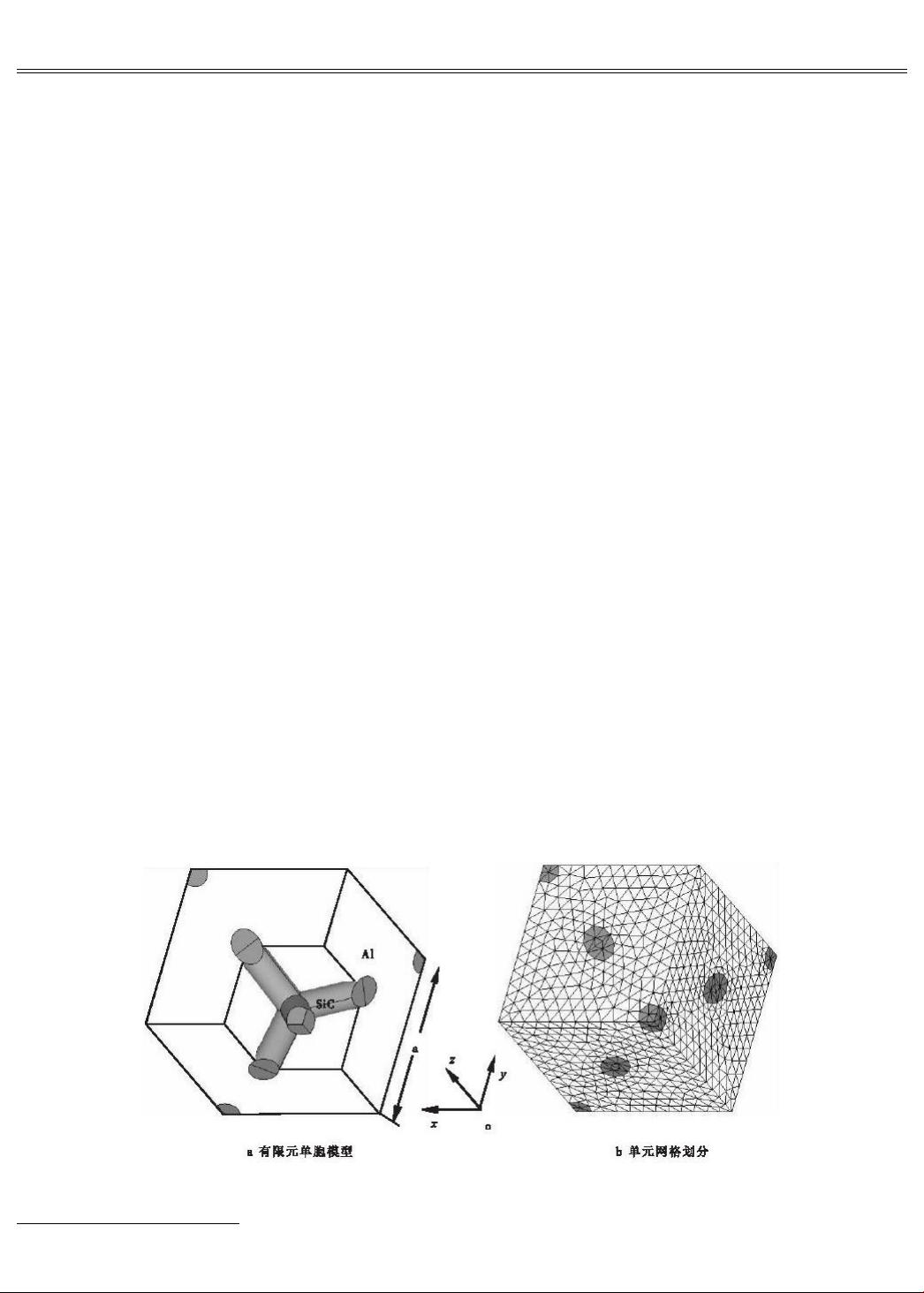 11. **三维有限元模型**：该论文采用的模型能够更精确地模拟实际的三维结构，对于分析网络状增强体特别有用，能够更好地预测材料性能。 这篇论文为理解和预测复合材料的弹性特性提供了一种新的有限元方法，特别是在三维网络增强复合材料领域，这对材料科学和工程应用具有重要意义。