0-1背包问题解析：递归与动态规划解法(C++)

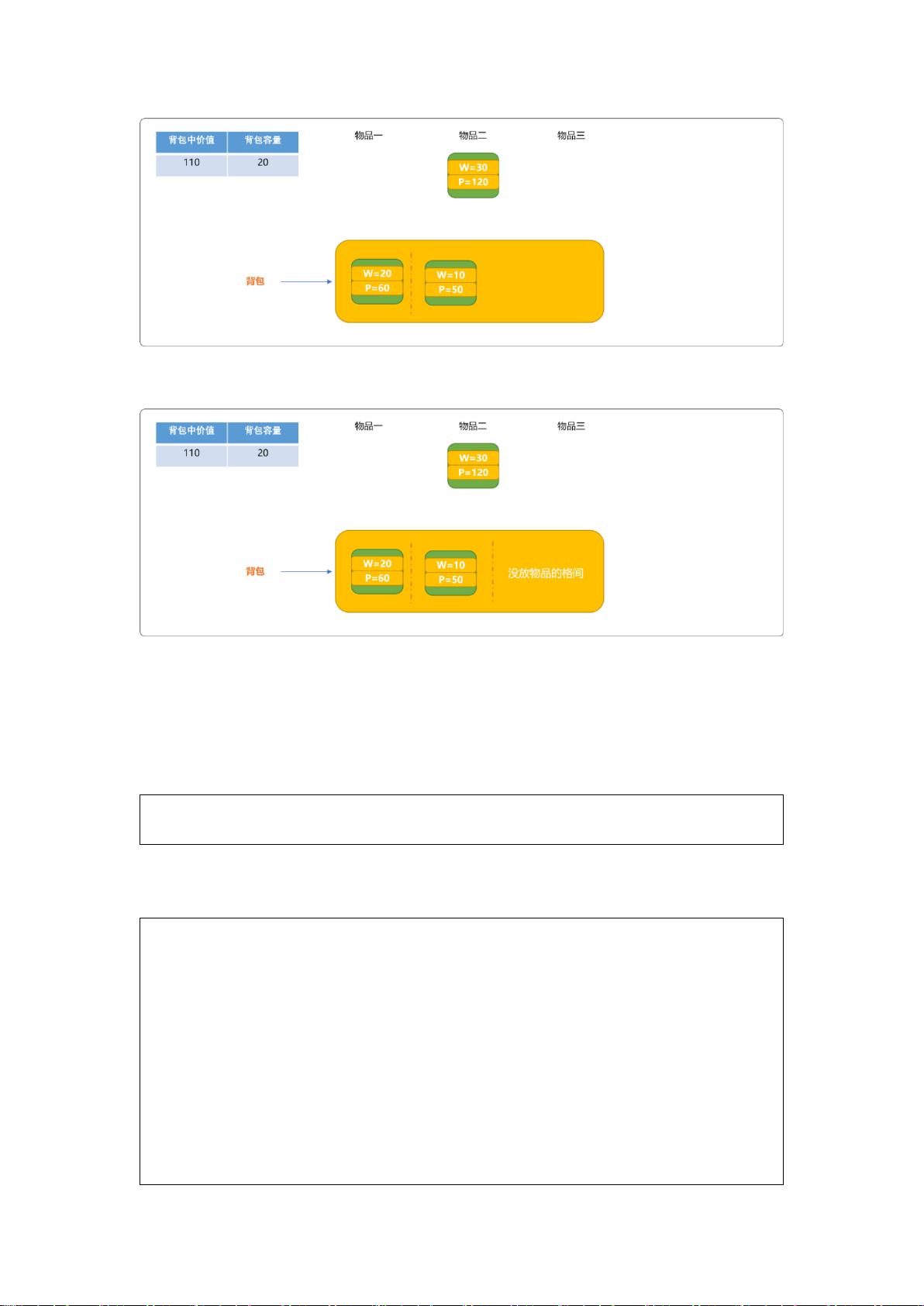
"这篇资料主要探讨了0-1背包问题的解决方案，重点介绍了两种方法：递归算法和动态规划。0-1背包问题是组合优化问题，目标是在不超过背包总容量的限制下，选取物品以最大化总价值。问题具有广泛的应用背景，如商业决策和计算复杂性理论等。资料中详述了递归算法的三种不同实现方式，并通过一个实例解释了回溯过程，展示了如何在物品无法放入或无剩余空间时进行回溯，以寻找最大价值的物品组合。" 0-1背包问题是一个经典的计算机科学问题，它涉及到在有限的资源约束下进行最优选择。在这个问题中，我们有n种物品，每种物品有自己的重量w[i]和价值v[i]，还有一个能承载最大重量m的背包。我们的目标是选择物品，使得在不超过背包总容量m的情况下，物品的总价值最大。 **1. 递归算法** 递归算法通常用于解决这类问题，它通过不断地尝试所有可能的子问题来寻找最优解。在0-1背包问题中，递归策略可以分为以下几步： 1.1.1 第一种递归回溯方案： - 如果背包容量为0或者所有物品都被考虑过，结束递归。 - 对于每个未被考虑过的物品i，有两种情况： - 不选择物品i，递归地处理剩余的背包容量和物品。 - 如果物品i的重量小于或等于剩余背包容量，选择物品i，然后递归地处理剩余的背包容量和剩余的物品。 - 在回溯过程中，比较并更新最大价值。 递归算法虽然直观，但效率较低，因为它会重复计算许多相同的子问题。 **2. 动态规划** 为了提高效率，可以采用动态规划（Dynamic Programming, DP）来解决0-1背包问题。动态规划通过存储之前计算的结果，避免了重复计算，提高了效率。 动态规划的状态通常定义为dp[j]，表示在容量为j的背包中能够达到的最大价值。状态转移方程可以表示为： dp[j] = max(dp[j], dp[j-w[i]] + v[i])，如果w[i] <= j，否则dp[j]保持不变。 从最小的背包容量开始，逐步增加，每次计算新容量下的最大价值，直到达到背包的最大容量。这样，最终的dp[m]就是背包容量为m时的最大价值。 动态规划的优点在于时间复杂度比递归算法显著降低，一般为O(n*m)，其中n是物品数量，m是背包容量。 0-1背包问题的解决方案展示了如何运用计算机科学的方法解决实际问题，无论是递归的直觉性还是动态规划的效率性，都能帮助我们找到最优的物品组合。通过深入理解和实践这两种方法，我们可以更好地理解和应用组合优化的策略，这对于理解和解决其他类似问题非常有帮助。