贪婪算法应用于工程项目的拓扑排序与路径规划

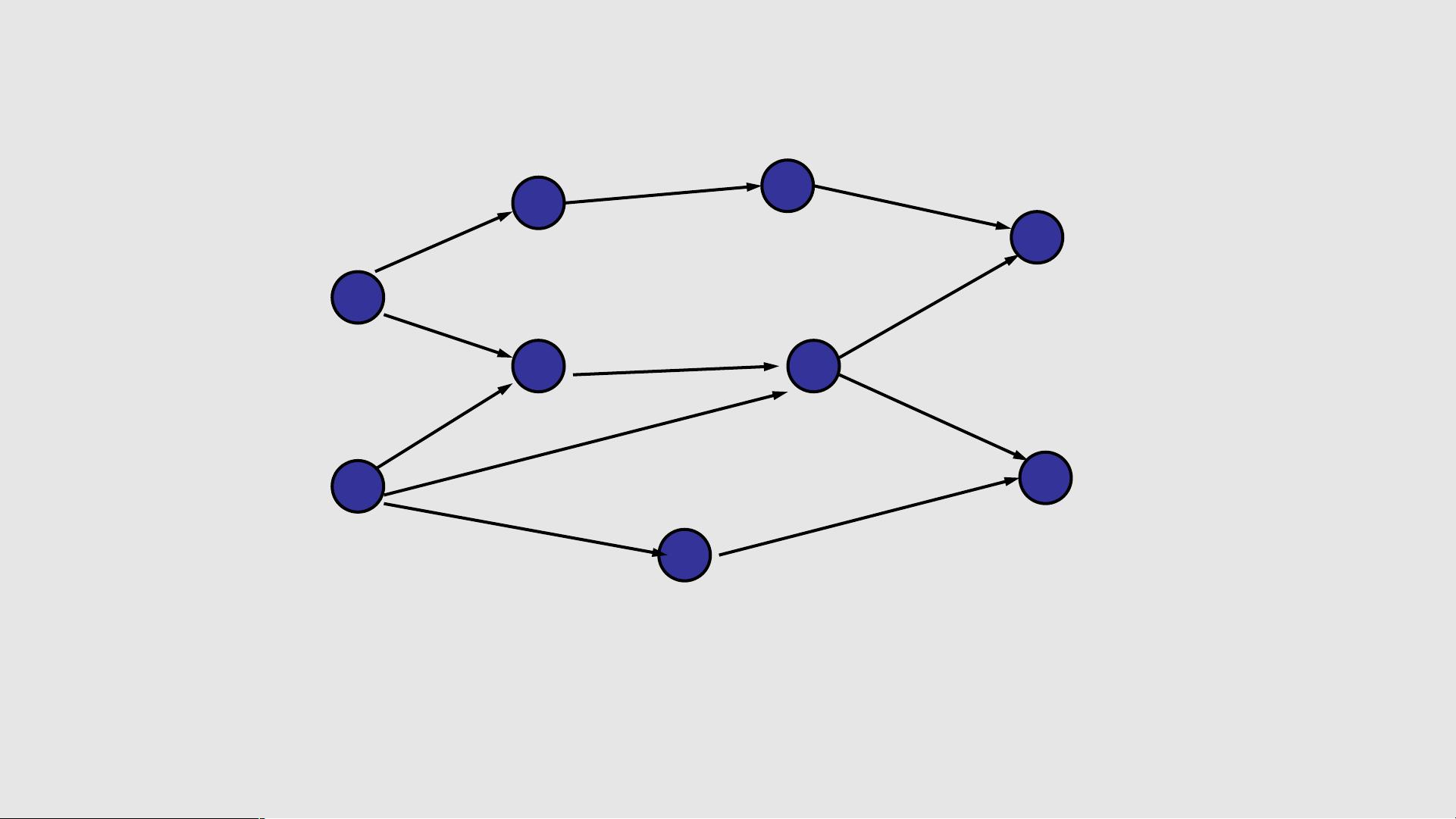
本文介绍了贪婪算法在不同应用场景下的使用，主要包括货箱装船、拓扑排序、单源最短路径和最小耗费生成树等方面。贪婪算法的思想是在每一步选择最优的解决方案，从而希望达到全局最优解。在货箱装船问题中，贪婪算法可以帮助优化装载货物的顺序，使得总运输成本最小化。在拓扑排序问题中，贪婪算法可以帮助确定工程活动的顺序，以便最快地完成整个工程。在单源最短路径和最小耗费生成树问题中，贪婪算法可以帮助找到最短路径或最小生成树，从而节省资源和时间。 拓扑排序是针对有向无环图(DAG)的一种排序算法，用于解决工程活动的顺序问题。在工程中，各个子工程之间通常存在着一定的约束关系，某些子工程必须在其他子工程完成后才能开始。通过拓扑排序，可以确定活动的顺序，保证工程能够按计划顺利进行，并且可以求解完成整个工程所需的最短时间。 在顶点表示活动的网络中，用有向图表示一个工程，顶点表示活动，有向边表示活动之间的先后关系。通过拓扑排序，可以得到一个活动顺序，使得每个活动的前驱活动都排在它的前面。拓扑排序还可以用来求解关键路径，即完成整个工程所需的最短时间，以便有效地安排资源和时间，确保工程的顺利进行和高效完成。 单源最短路径问题是在一个加权有向图或无向图中，寻找从一个固定节点到其他所有节点的最短路径。Dijkstra算法是一种贪婪算法，通过不断选择当前离源节点最近的节点来更新最短路径，直到所有节点都被访问过。Dijkstra算法的时间复杂度为O(V^2)，其中V为节点的数量，适用于稠密图。另外，最小耗费生成树问题是在一个带权无向图中，寻找一棵包含所有节点的生成树，使得树的边权之和最小。Kruskal算法、Prim算法和Sollin算法都是贪婪算法，用于求解最小耗费生成树问题，通过不断选择权值最小的边来构建最小生成树。 总而言之，贪婪算法在各种实际应用中都有着重要的作用，能够帮助解决各种优化问题，如货箱装船、工程活动排序、最短路径和最小生成树等。通过选择当前最优的解决方案，贪婪算法可以在很短的时间内找到一个近似最优解，有效地提高了问题的求解效率和准确性。因此，贪婪算法是一种实用而有效的算法思想，在实际工程和科学研究中有着广泛的应用前景。