非参数密度估计：Parzen窗与k-NN方法

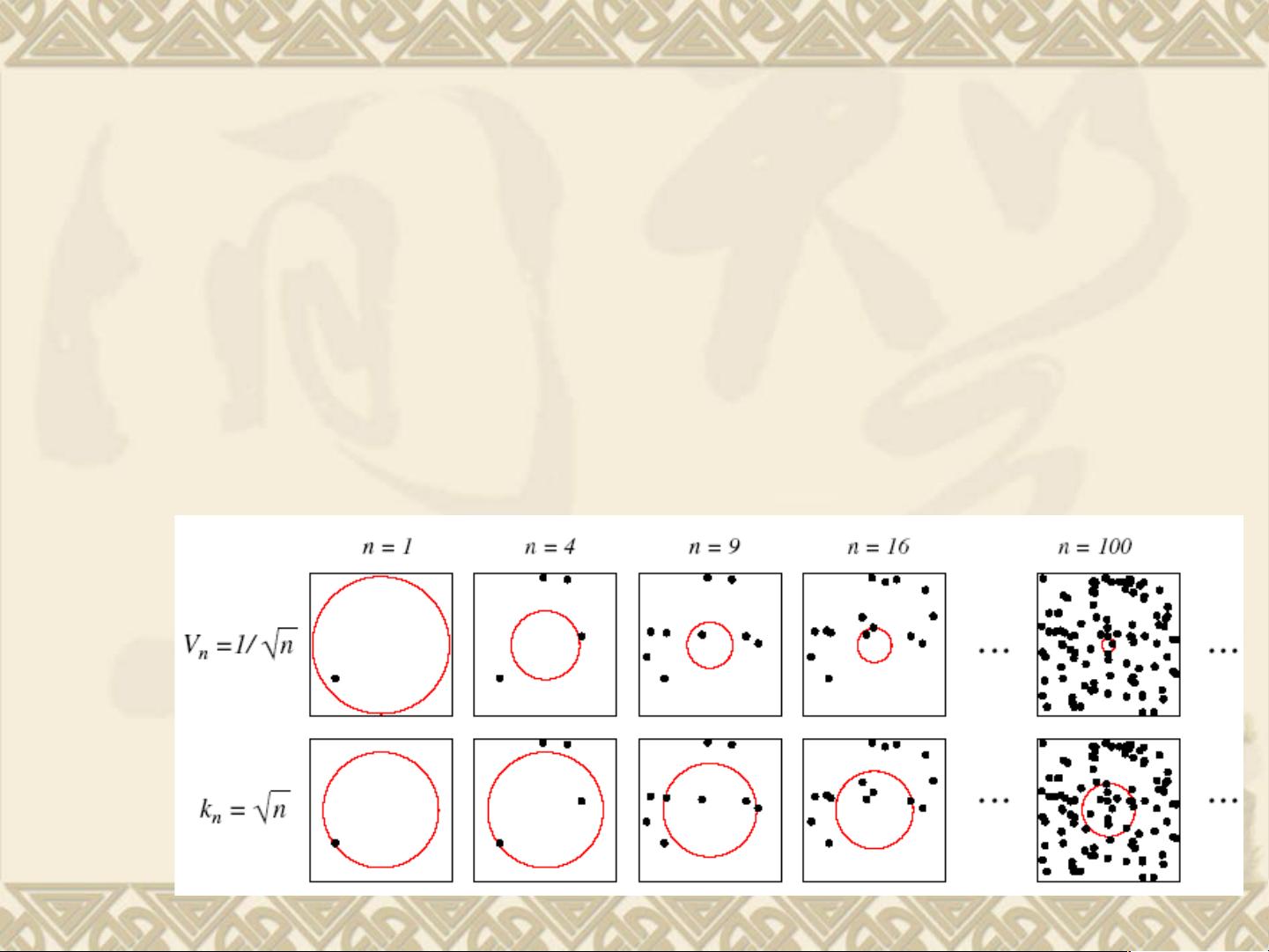
"非参数估计方法，特别是Parzen窗估计和k-NN估计在概率密度估计及分类中的应用" 非参数估计是一种统计方法，用于估计未知的概率分布，它不依赖于预先设定的概率密度函数形式。这种方法在实际问题中非常有用，因为很多情况下，我们无法准确地知道数据遵循的具体概率模型。非参数估计可以处理多模态分布、高维数据以及那些不能简单分解为低维函数乘积的情况。 概率密度估计是寻找数据分布形状的过程，对于独立同分布(i.i.d.)的样本集，目标是找到一个能够描述这些样本的分布的函数。直方图是最简单的非参数密度估计方法，通过将数据空间划分为小的区间（或“小窗”），然后计算每个区间内样本的数量，并除以总样本数和区间体积来估计区间内的密度。 Parzen窗估计，也称为窗口密度估计，是通过在每个样本点周围放置一个有特定宽度的窗口（通常选择高斯窗口或Epanechnikov窗口），然后用窗口函数的积分来估计密度。窗口函数的选择会影响估计的平滑程度。对于足够大的样本量和适当的窗口大小，Parzen窗估计可以提供对概率密度函数的精确估计。 k-NN（最近邻）估计是另一种非参数方法，它基于一个简单的思想：一个点的密度可以由其最近的k个邻居的密度来估计。k-NN不仅用于密度估计，也被广泛应用于分类任务，即k-NN分类器。在这个分类器中，新样本的类别是其最近的k个邻居中最常见的类别。k值的选择对结果有显著影响，较小的k值可能导致过拟合，较大的k值则可能导致欠拟合。 最近邻分类器（NN）是k-NN的一个特殊情况，当k=1时，分类决策基于与新样本最近的一个训练样本的类别。NN分类器简单直观，但可能对噪声和异常值敏感。 非参数估计方法的主要优点在于其灵活性，能够适应各种复杂的数据分布，而无需进行严格的模型假设。然而，它们也有局限性，例如样本需求量大，计算成本高，以及对异常值和边界效应敏感。在实际应用中，需要根据具体问题选择合适的非参数方法，并通过调整参数（如窗口大小、k值等）来优化性能。