is document classification, and each term is taken as a binary
feature, then X is the space of all term vectors, x
i
is the ith term
vector corresponding to some documents, and X is a
particular learning sample. In general, if two domains are
different, then they may have different feature spaces or
different marginal probability distributions.
Given a specific domain, D¼fX;PðXÞg,atask consists
of two components: a label space Y and an objective
predictive function fðÞ (denoted by T¼fY;fðÞg), which is
not observed but can be learned from the training data,
which consist of pairs fx
i
;y
i
g, where x
i
2 X and y
i
2Y. The
function fðÞ can be used to predict the corresponding label,
fðxÞ, of a new instance x. From a probabilistic viewpoint,
fðxÞ can be written as PðyjxÞ. In our document classification
example, Y is the set of all labels, which is True, False for a
binary classification task, and y
i
is “True” or “False.”
For simplicity, in this survey, we only consider the case
where there is one source domain D
S
, and one target domain,
D
T
, as this is by far the most popular of the research works in
the literature. More specifically, we denote the source domain
data as D
S
¼fðx
S
1
;y
S
1
Þ; ...; ðx
S
n
S
;y
S
n
S
Þg, where x
S
i
2X
S
is
the data instance and y
S
i
2Y
S
is the corresponding class
label. In our document classification example, D
S
can be a set
of term vectors together with their associated true or false
class labels. Similarly, we denote the target-domain data as
D
T
¼fðx
T
1
;y
T
1
Þ; ...; ðx
T
n
T
;y
T
n
T
Þg, where the input x
T
i
is in
X
T
and y
T
i
2Y
T
is the corresponding output. In most cases,
0 n
T
n
S
.
We now give a unified definition of transfer learning.
Definition 1 (Transfer Learning). Given a source domain D
S
and learning task T
S
, a target domain D
T
and learning task
T
T
, transfer learning aims to help improve the learning of the
target predictive function f
T
ðÞ in D
T
using the knowledge in
D
S
and T
S
, where D
S
6¼D
T
,orT
S
6¼T
T
.
In the above definition, a domain is a pair D¼fX;PðXÞg.
Thus, the condition D
S
6¼D
T
implies that either X
S
6¼X
T
or
P
S
ðXÞ 6¼ P
T
ðXÞ. For example, in our document classification
example, this means that between a source document set and
a target document set, either the term features are different
between the two sets (e.g., they use different languages), or
their marginal distributions are different.
Similarly, a task is defined as a pair T¼fY;PðY jXÞg.
Thus, the condition T
S
6¼T
T
implies that either Y
S
6¼Y
T
or
P ðY
S
jX
S
Þ 6¼ P ðY
T
jX
T
Þ. When the target and source domains
are the same, i.e., D
S
¼D
T
, and their learning tasks are the
same, i.e., T
S
¼T
T
, the learning problem becomes a
traditional machine learning problem. When the domains
are different, then either 1) the feature spaces between the
domains are different, i.e., X
S
6¼X
T
, or 2) the feature spaces
between the domains are the same but the marginal
probability distributions between domain data are different;
i.e., P ðX
S
Þ 6¼ P ðX
T
Þ, where X
S
i
2X
S
and X
T
i
2X
T
.Asan
example, in our document classification example, case 1
corresponds to when the two sets of documents are
described in different languages, and case 2 may correspond
to when the source domain documents and the target-
domain documents focus on different topics.
Given specific domains D
S
and D
T
, when the learning
tasks T
S
and T
T
are different, then either 1) the label
spaces between the domains are different, i.e., Y
S
6¼Y
T
,or
2) the conditional probability distributions between the
domains are different; i.e., P ðY
S
jX
S
Þ 6¼ P ðY
T
jX
T
Þ, where
Y
S
i
2Y
S
and Y
T
i
2Y
T
. In our document classification
example, case 1 corresponds to the situation where source
domain has binary document classes, whereas the target
domain has 10 classes to classify the documents to. Case 2
corresponds to the situation where the source and target
documents are very unbalanced in terms of the user-
defined classes.
In addition, when there exists some relationship, explicit
or implicit, between the feature spaces of the two domains,
we say that the source and target domains are related.
2.3 A Categorization of
Transfer Learning Techniques
In transfer learning, we have the following three main
research issues: 1) what to transfer, 2) how to transfer, and
3) when to transfer.
“What to transfer” asks which part of knowledge can be
transferred across domains or tasks. Some knowledge is
specific for individual domains or tasks, and some knowl-
edge may be common between different domains such that
they may help improve performance for the target domain or
task. After discovering which knowledge can be transferred,
learning algorithms need to be developed to transfer the
knowledge, which corresponds to the “how to transfer” issue.
“When to transfer” asks in which situations, transferring
skills should be done. Likewise, we are interested in
knowing in which situations, knowledge should not be
transferred. In some situations, when the source domain
and target domain are not related to each other, brute-force
transfer may be unsuccessful. In the worst case, it may
even hurt the performance of learning in the target
domain, a situation which is often referred to as negative
transfer. Most current work on transfer learning focuses on
“What to transfer” and “How to transfer,” by implicitly
assuming that the source and target domains be related to
each other. However, how to avoid negative transfer is an
important open issue that is attracting more and more
attention in the future.
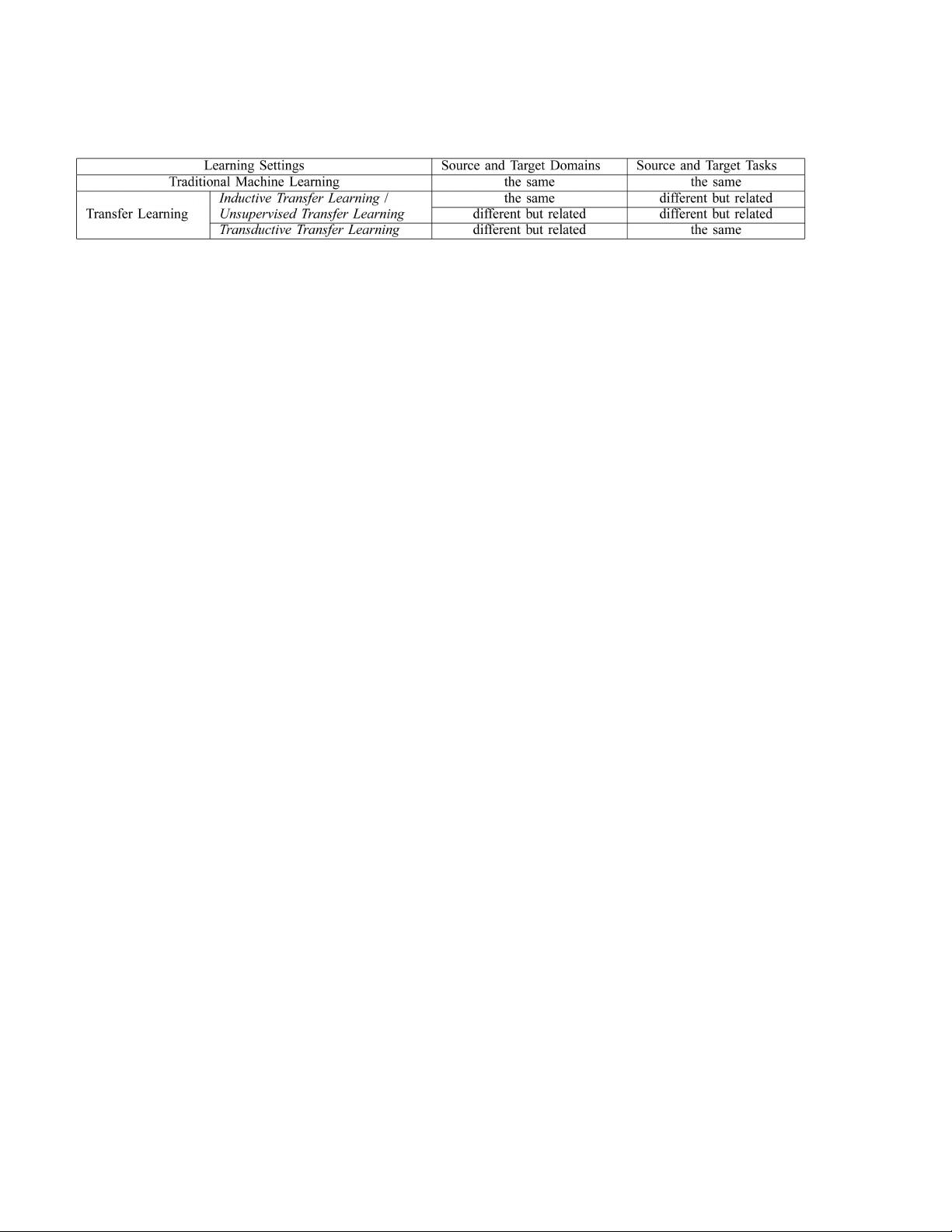
Based on the definition of transfer learning, we summarize
the relationship between traditional machine learning and
various transfer learning settings in Table 1, where we
PAN AND YANG: A SURVEY ON TRANSFER LEARNING 1347
TABLE 1
Relationship between Traditional Machine Learning and Various Transfer Learning Settings









