Bethe Ansatz方法计算p+ip配对模型的开放与封闭系统基态能量

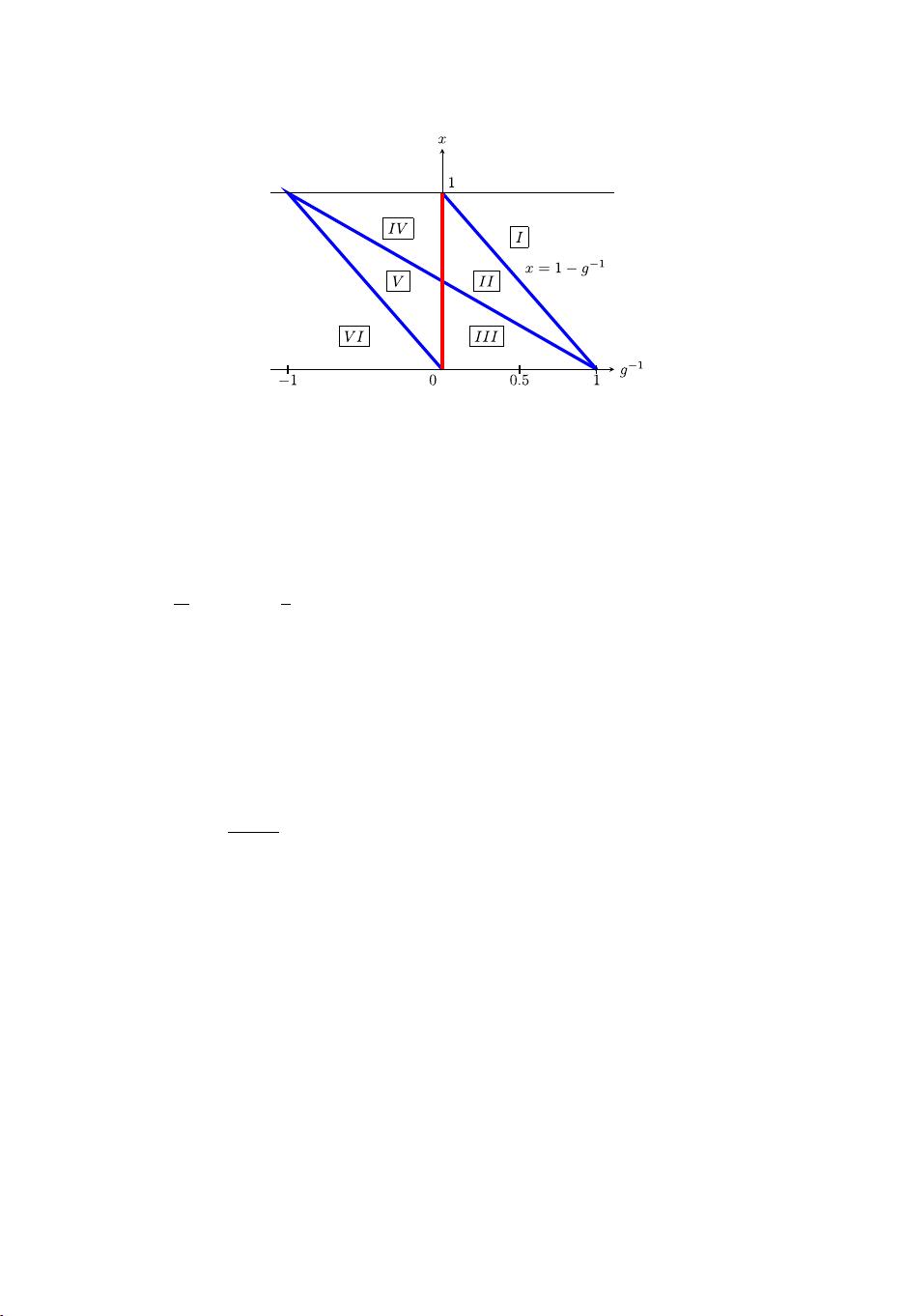
本文主要探讨了Bethe Ansatz方法在计算开放和封闭的p+ip配对模型的基态能量中的应用。Bethe Ansatz是一种强大的工具，在量子许多体系统中用于解析求解特定类型的模型，特别是在统计力学和凝聚态物理中处理一维量子链问题。在这个背景下，研究者们针对p+ip配对模型，这是一种重要的超导理论模型，其中电子的自旋和动量配对形成一种特殊的相。 首先，文章关注的是封闭模型，即哈密顿量被隔离于其环境之外，这种情况下的Bethe Ansatz解通常涉及到复数的Bethe根。这些根是Bethe Ansatz方程的解，它们与系统的量子态和能量密切相关。作者通过连续极限逼近法，将复杂的Bethe方程转化为积分方程，这是一种数值上可处理的有效工具，可以用来估计基态能量。这种方法依赖于系统的参数变化，它揭示了根分布曲线随参数改变的行为，但同时也探讨了这种近似方法的局限性。 接着，文章转向了一种不同的计算策略，即通过某种技术将Bethe Ansatz方程转换成更容易分析的形式。这可能涉及到数学上的变换技巧，如变换变量、归一化或者利用特殊函数的性质，以便简化计算并获取更准确的结果。这种转换可能有助于克服前一种方法在某些参数区域的困难，或者提供额外的物理洞察。 整个研究过程旨在深入理解p+ip配对模型的基础性质，特别是其基态的能量特性，这对于理解超导现象以及相关材料的性质至关重要。作者Yibing Shen、Phillip S. Isaac和Jon Links通过对这两种方法的比较和讨论，不仅展示了Bethe Ansatz的强大之处，也揭示了理论物理中数值计算和解析方法的互补性。 本文的核心内容涵盖了Bethe Ansatz的理论基础，从封闭模型的复数Bethe根到实际计算中的连续极限和积分方程，再到不同策略对基态能量计算的影响。这项工作对于那些从事低维度量子系统、超导物理学或Bethe Ansatz方法研究的科学家来说，提供了宝贵的参考和深入学习的素材。