维纳滤波详解：最小均方误差估计

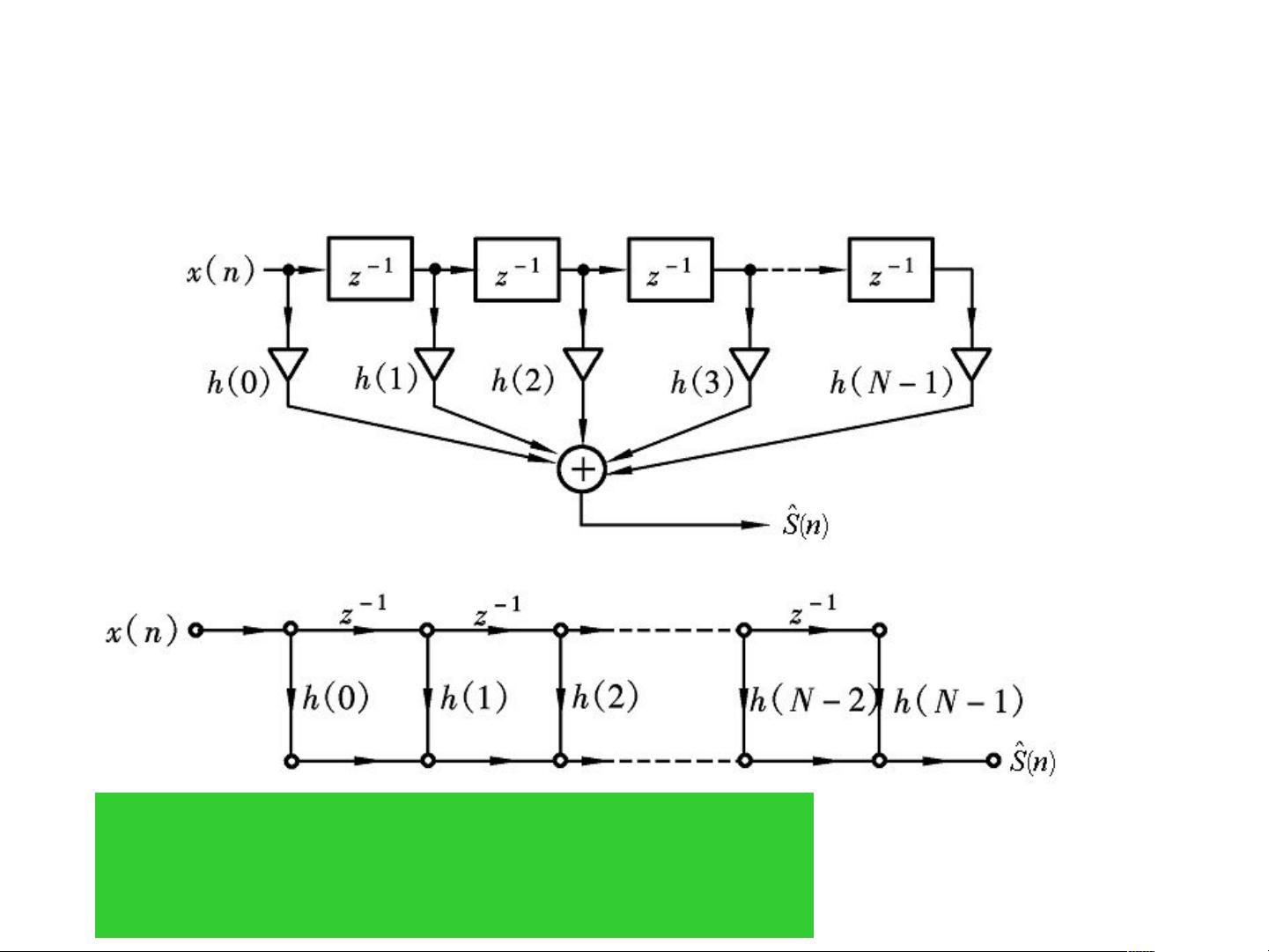
“中文 维纳滤波.ppt”是一份详细介绍维纳滤波理论和应用的资料，涵盖了从基本概念到实际计算案例的多个方面。 维纳滤波是数字信号处理领域中的一种重要技术，主要用于对真实信号进行最小均方误差（MMSE）估计。在信号处理过程中，我们通常面临的问题是：如何通过观测到的带有噪声的数据恢复原始信号。维纳滤波提供了解决这个问题的一个有效框架。它包括了对信号的平滑、滤波和预测等操作。 1.1 维纳滤波问题描述 维纳滤波关注的是如何设计一个滤波器，该滤波器可以将观测数据转化为对真实信号的最优估计，即最小化估计误差的均方值。在噪声存在的情况下，这一目标可以通过线性滤波器来实现，滤波器的系数由维纳滤波理论确定。 1.2 维纳FIR滤波器与维纳非因果IIR滤波器 维纳FIR滤波器是有限 impulse response（FIR）结构的滤波器，其单位冲激响应是有限长度的。而非因果IIR滤波器则不受因果性的限制，可能包含未来的信号值，但不适用于实时处理。 1.3 维纳因果IIR滤波器 在实际应用中，我们通常需要考虑因果滤波器，即滤波器的输出只依赖于当前及过去的输入样本。维纳因果IIR滤波器就是满足这一条件的滤波器，它在保持最小均方误差估计的同时，确保了滤波器的实时性。 1.4 深入了解的预备知识 学习维纳滤波之前，需要掌握线性代数、概率论和随机过程的基础知识，以及信号与系统的概念，这些是理解和设计维纳滤波器所必需的。 1.5 维纳IIR滤波器计算例子 这部分内容可能详细阐述了如何计算维纳IIR滤波器的系数，通过具体的数学公式和步骤展示了如何求解滤波器参数。 1.6 维纳预测器 维纳预测器是维纳滤波理论在预测领域的应用，它可以根据已有的数据预测未来的时间序列，同样基于最小化预测误差的均方值。 在实际应用中，维纳滤波被广泛用于图像去噪、信号恢复、时间序列分析等多个领域。通过解决线性估计问题，维纳滤波能够提供一种优化的解决方案，即使在噪声环境复杂的情况下也能得到较好的结果。理解并掌握维纳滤波的原理和实现方法对于从事信号处理和数据分析的专业人士来说至关重要。