SPSS中逻辑回归实战：理解参数与建模过程

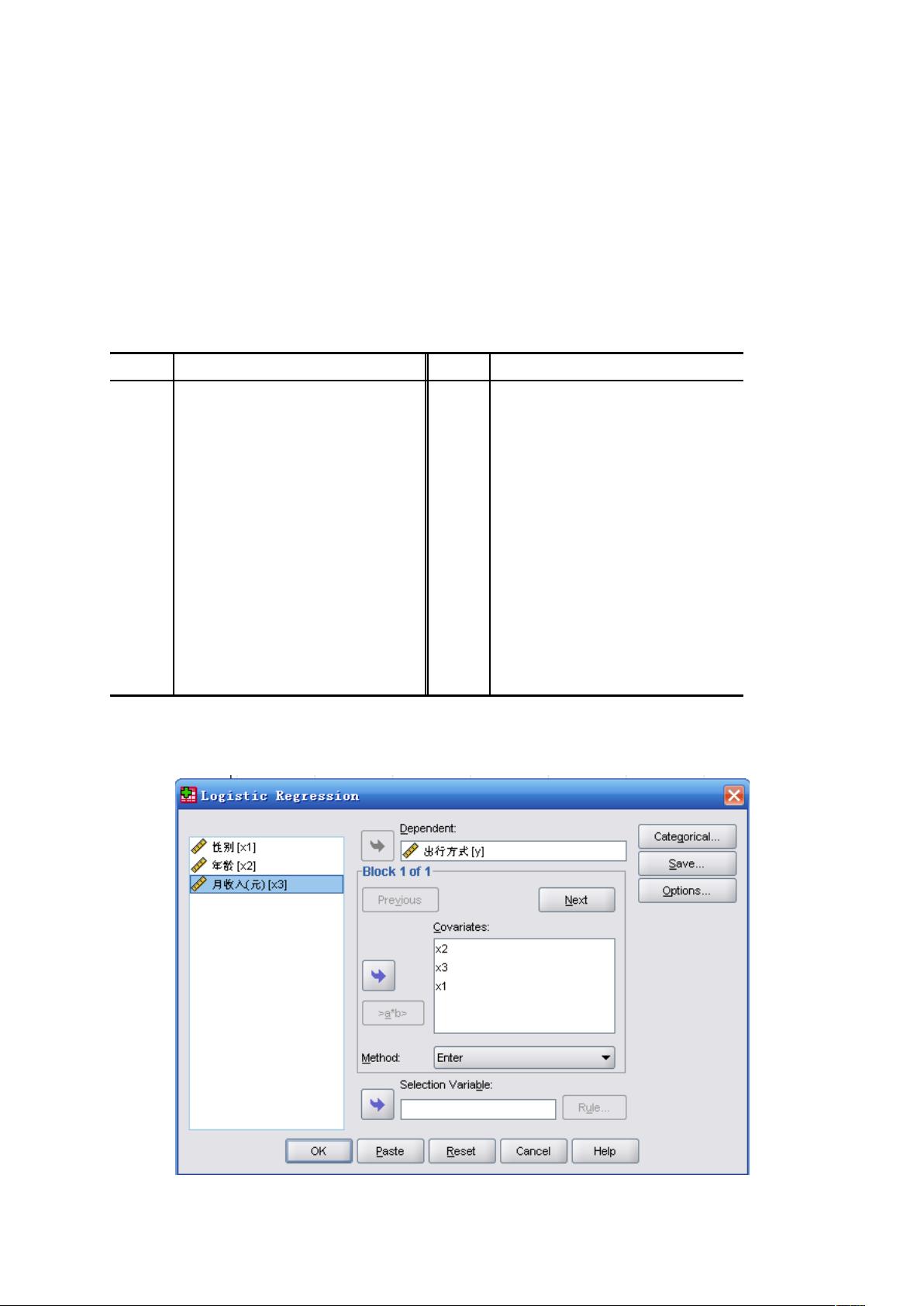
本资源主要介绍了如何在SPSS中实现逻辑回归（Logistic Regression）的具体步骤，并解释了相关参数的含义。首先，逻辑回归是一种用于二分类问题的统计学方法，它通过将线性回归模型的输出转换为概率形式来预测离散结果。在给出的社会调查例子中，研究者想要了解年龄、月收入和性别（X1, X2, X3）是否能预测人们选择乘坐公交车（Y=1）还是骑自行车（Y=0）上班。 1. 数据概述：提供的数据包含28个工薪族样本，其中无缺失值。表8-4展示了案例的分类和因变量编码，以及初始的-2对数似然值（-2LL），表示模型的拟合度。 2. 模型构建过程： - 第一步：建立了只包含常数项的模型，-2LL值为38.673，表示当前模型的拟合效果。 - 进入迭代过程：在后续步骤中，逐步加入了自变量X1（年龄）、X2（月收入），并在达到一定准则（参数估计变化小于0.001）后停止迭代。 - 最终模型在步骤5处终止，-2LL值进一步降低，显示模型加入了自变量后的拟合性增强。 3. 结果检验：表7展示了迭代历史记录，每次迭代的-2LL值和系数值变化。卡方检验（表8）用于评估模型整体的拟合优度，其显著性水平为0.005，表明模型与观测数据之间存在显著关联。 4. 分类表（表4）给出了预测结果，根据预测值和切割值（此处为0.500），可以判断每个观测值落入哪一类（0表示骑车，1表示乘车）。 5. 变量重要性：表5列出了模型中的变量及其得分，df（自由度）也一并列出，这些信息可用于判断每个自变量对结果的影响程度。 这个资源详细讲解了如何使用SPSS进行逻辑回归分析，包括数据预处理、模型建立、迭代过程和结果解释等关键步骤，对于理解和应用逻辑回归技术非常有帮助。在实际应用中，理解这些参数和表格有助于优化模型并确保其在预测上的有效性。