遗传算法求解六次函数极值：MATLAB仿真实例

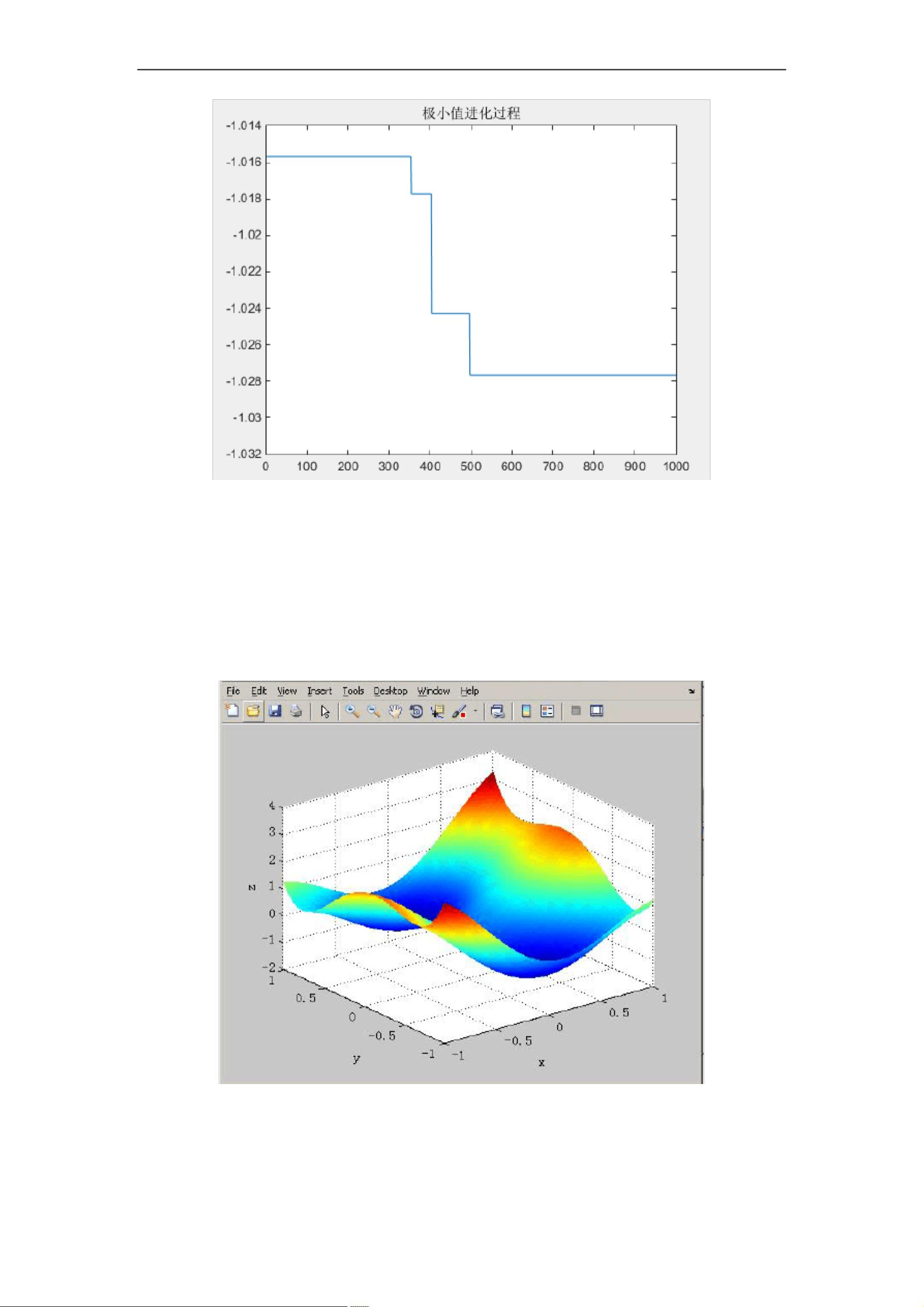
本文档主要探讨了如何使用MATLAB进行人工智能领域的函数优化问题，特别是通过遗传算法来解决一个具有六个极值点的二元六次函数。遗传算法是一种基于生物进化原理的优化方法，它在解决复杂全局优化问题时表现出通用性、并行性、稳健性和全局优化能力强的特点。 首先，设计思路部分介绍了遗传算法的基本工作原理，包括选择算子（根据适应度选择优秀的个体）、交叉算子（模拟基因重组，产生新个体）和变异算子（随机改变个体的某些基因），这些操作用于种群的进化。目标是找到函数的极值点，这里是二元函数f(x,y) = 4x^2 - 2.1x^4 + (1/3)x^6 + x*y - 4y^2 + 4y^4。 程序流程图展示了遗传算法的具体步骤：从问题的初始解（这里是个体的染色体表示）开始，通过编码、种群的选择与更新（包括适应度评估、复制、交叉和变异）、遗传运算的迭代，直至种群达到预设的优化标准。实验程序`objectFunction`定义了评估函数值的过程，其核心是计算给定种群中每个个体的适应度，即函数值。 文档还包含了MATLAB代码实现细节，如交叉率（pc）、变异率（pm）、个体数目（NIND）、最大遗传代数（MAXGEN）、变量维数（NVAR）、变量精度（PRECI）、代沟（GGAP）以及种群初始化过程，使用`rep`、`crtbp`和`bs2rv`等函数进行操作。 具体到实验部分，初始化阶段设置了算法参数，并通过`bs2rv`函数将二进制形式的种群转换为十进制，然后计算第一代的函数适应度，记录下每代的极小值和极大值。通过反复迭代，直到达到最大遗传代数或种群满足预设的优化标准，最终找到函数的极值点。 这份文档提供了如何利用MATLAB中的遗传算法对复杂的多峰函数进行优化的实例，展示了从问题定义、算法原理到实际编程的完整过程，对希望学习和实践人工智能优化技术的学生和研究者具有很高的参考价值。