模拟退火算法在大规模优化中的应用

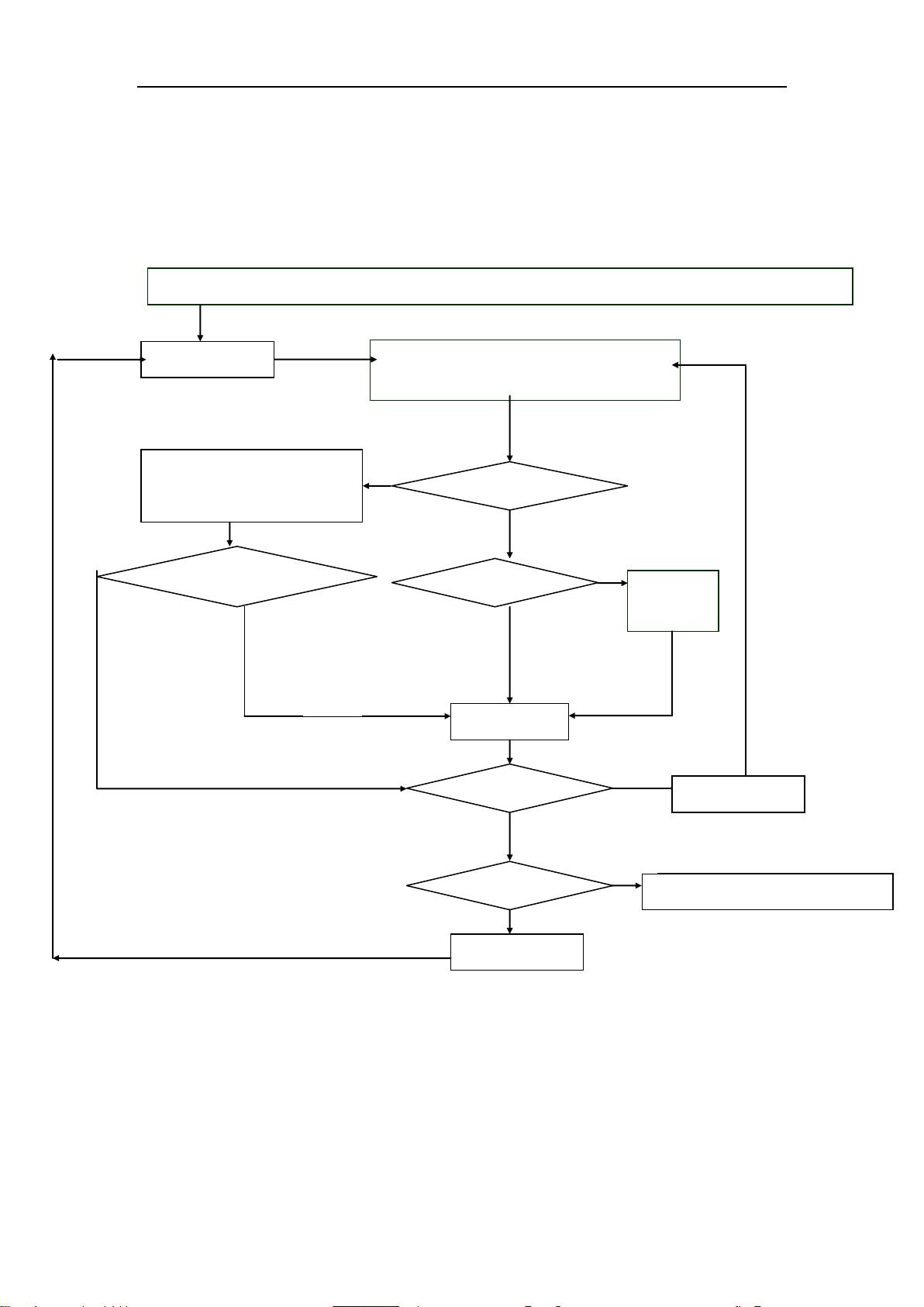
"第二章-模拟退火算法讨论了如何运用物理退火过程的原理解决最优化问题。模拟退火算法由Kirkpatrick等人在1982年提出，主要针对NP完全问题，能提供近似最优解。算法借鉴了固态退火的原理，通过Metropolis接受准则和冷却进度表调整搜索过程。物理退火包括加热、熔解和有序冷却阶段，其中快速冷却可能导致非最优的亚稳态。在等温过程中，系统遵循Boltzmann的有序性原理，即自由能最小化。Metropolis算法是Monte Carlo技术的一种，用于模拟恒温下物质达到热平衡，虽然需要大量计算但能探索低能量状态。" 在智能优化领域，模拟退火算法是一种重要的技术。该算法的核心是模拟物理退火过程中固体从高温到低温的转变，以此解决复杂优化问题。首先，系统被加热至极高温度，此时所有可能的状态都有可能出现，这对应于优化问题的初始阶段，允许算法探索广泛的解决方案空间。然后，系统逐渐冷却，类似于算法逐步缩小搜索范围，更倾向于接受低能量（或低代价）的状态。 Metropolis算法是模拟退火算法的关键组成部分，它基于蒙特卡洛方法，允许算法在一定的概率下接受更高能量（或更高代价）的解决方案，这是为了避免算法过早陷入局部最优解。这一概率随着系统的冷却而逐渐降低，使得算法能够在接近最优解时更加保守，从而找到全局最优或近似最优解。 冷却进度表是模拟退火算法的另一个关键元素，它定义了温度随时间（迭代次数）降低的速度。合适的冷却进度表设计能够确保算法在不同阶段有足够的探索性和收敛性，既能在初期广泛探索，又能在后期有效收敛。 在实际应用中，模拟退火算法通常用于解决旅行商问题、图着色问题、作业调度等NP完全问题。尽管计算量较大，但其灵活性和对全局最优解的寻找能力使其在解决复杂优化问题时具有优势。模拟退火算法是结合了物理理论与计算机科学的一门强大技术，为解决实际中最优化挑战提供了有效工具。