图论与算法入门：从七桥问题到现代应用

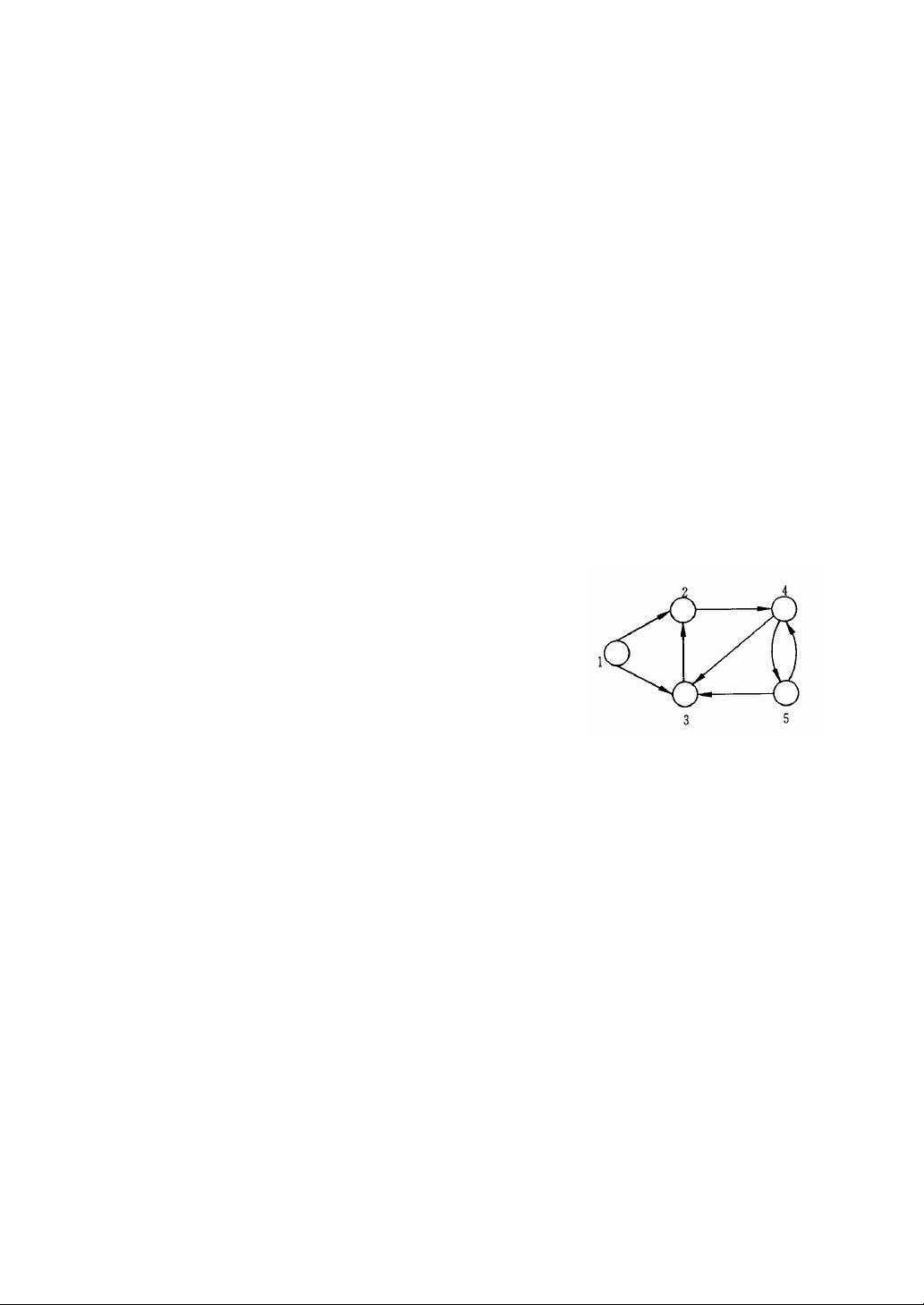
"本文介绍了图论及其算法的基础知识，适合初学者学习。图论起源于18世纪，随着计算机技术的发展，其应用已广泛渗透到多个学科。文章以哥尼斯堡七桥问题为例，阐述了如何用图论建模解决问题，并提到了图论中的基本概念，如点、线和连通性。此外，还提及了图与网络在运筹学中的重要地位，以及一些典型的问题，如最短路问题，这些都是图论在实际应用中的核心问题。" 在图论中，"图"是由点（顶点）和连接点的边（或线）构成的抽象结构，用于表示事物间的关系。欧拉通过将哥尼斯堡的四块陆地和七座桥转化为图模型，提出了判断一笔画问题的准则，即图是连通的，且每个点的度数（与之相连的边数）为偶数。这一准则不仅解决了七桥问题，也为后续的图论研究奠定了基础。 图的类型包括简单图、有向图、无向图、加权图等，每种类型都有其特定的应用场景。例如，有向图常用于表示流程的方向，加权图则可以用于表示各边的重要性或成本。在实际问题中，图论的应用包括但不限于最短路径寻找、网络流量优化、社交网络分析、遗传学中的分子结构分析等。 图的算法是解决这些问题的关键工具，其中包括著名的Dijkstra算法和Floyd-Warshall算法，它们分别用于求解单源最短路径和所有对最短路径问题。最大流问题和最小费用流问题则涉及网络中的流量分配，通常采用Ford-Fulkerson算法或Edmonds-Karp算法解决，旨在找到网络中能通过的最大流量或最小成本流量。 匹配问题在图论中也有重要地位，如匈牙利算法用于解决完全匹配问题，而在二分图中，Kuhn-Munkres算法（Kuhn-Munkres算法，又称KM算法）可以找到最大匹配。 图论及其算法是解决复杂关系网络问题的有效数学工具，它的理论深度和广泛应用使其成为计算机科学、运筹学、工程和自然科学等领域的重要研究内容。对于初学者而言，理解并掌握这些基本概念和算法，将有助于解决实际中的许多挑战。