8262 IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 65, NO. 10, OCTOBER 2018
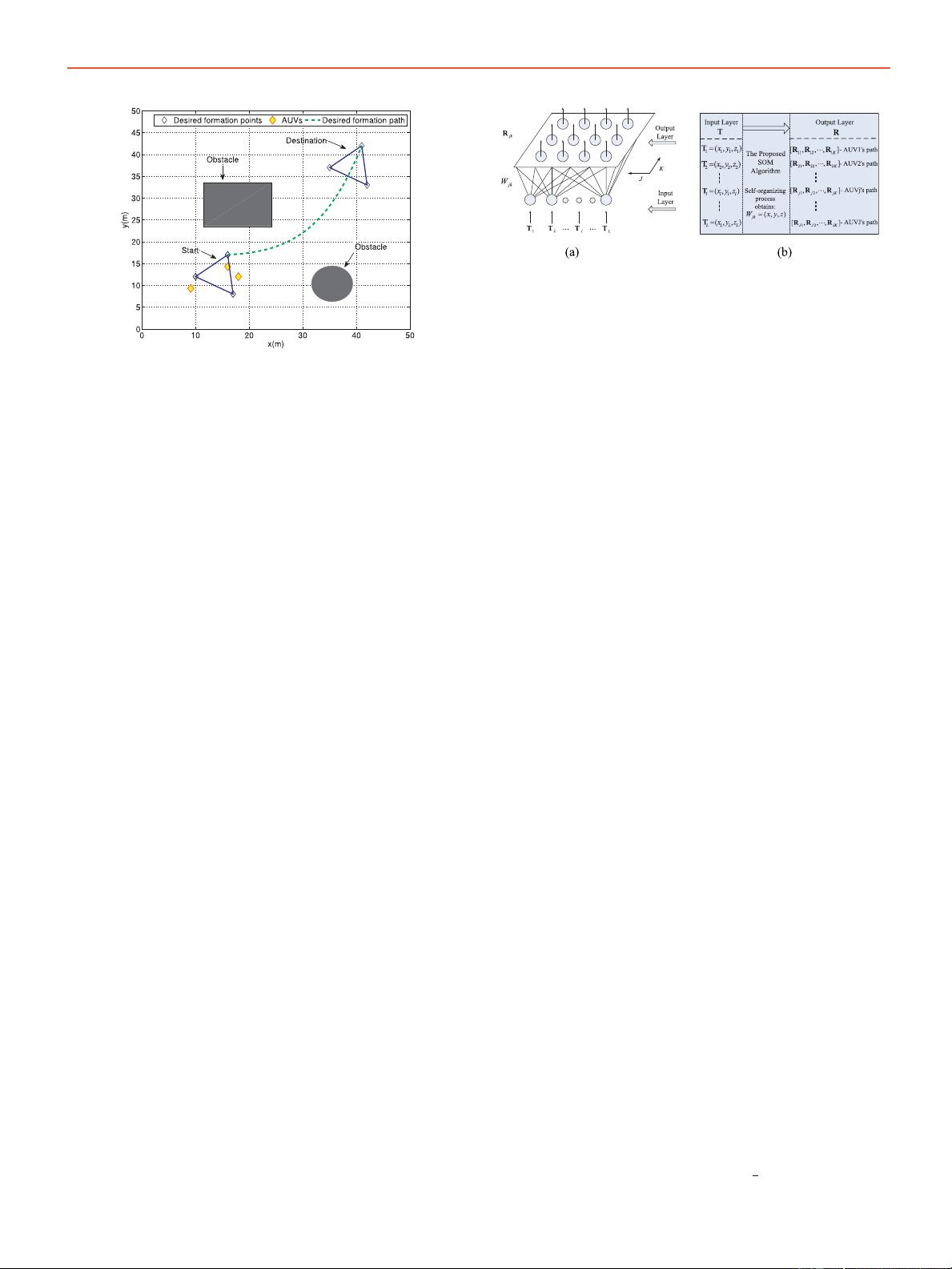
Fig. 1. Plan view of a tr i angular formation example with three randomly
distributed AUVs.
reduction of the total traveling cost and the workload balance of
every single AUV are taken into consideration.
B. Thinking in SOM
The SOM neural network method was first introduced by T.
Kohonen in the 1980s and extended later [32]–[34]. It is based
on the idea that there is a special order of processing units in
the mammalian brain. Each unit is dedicated to a specific task
and each group of neurons is sensitive to a particular type of
input signal. The units are determined by parameters that can be
changed in certain processes to produce meaningful organiza-
tions. This algorithm soon became a valuable tool and was used
to solve many kinds of problems. In recent years, this method
has been applied to solve task assignment problems and control
of multirobot systems [35]–[38].
In this paper, we develop an SOM-based approach that could
be applied to the formation-control problems by improving the
previous SOM method. The idea comes from the similar char-
acteristics and phenomena between a multi-AUV system and an
SOM network. First, a multi-AUV formation system is the same
as a self-organizing system that only changes its inner structure.
Second, the SOM algorithm has the competitive, cooperative,
and self-organizing characteristics that are attractive for a multi-
AUV system. Thus, the SOM network could be adapted to an
unordered team of AUVs to automatically achieve the desig-
nated locations with cooperation and competition. The AUV
formation could be achieved in this way. By the formation-
tracking strategy, the movement and tracking of the formation
is also realized. In this paper, we propose an improved workload
function, which makes sure that the traveling length of a single
AUV is balanced within a limited range.
An SOM-based neural network model is shown in Fig. 2(a),
and the mapping relationship is shown in Fig. 2(b). The proposed
algorithm could be executed within a reasonable computation
time, emphasizing on workload balance for each AUV in the
team. At the initial state, there are J AUVs randomly distributed
in the workspace, where J ∈ N
+
. L points are set at the key
positions of the expected formation shape. For instance, there
are three points to form a triangle as Fig. 1 illustrates, so that we
Fig. 2. Structure of SOM Neural Network. (a) The structure (T
l
: coordi-
nates of the lth point; R
jk
: coordinates of AUV at a certain time instant).
(b) Mapping relationship of the two layers.
obtain L =3. In this way, the SOM model has two layers of neu-
rons. The first layer is the input layer including L neurons, where
L ∈ N
+
. These neurons represent the Cartesian coordinates of
the points in the 3-D workspace. T is a 3 × L matrix that de-
notes the coordinates of the target points as input neurons. Each
input neuron has three parameters (x
l
,y
l
,z
l
) according to the
coordinates of its corresponding point, where l =1, 2,...,L.
All the coordinates of the points form the input data set. The
second layer is the output layer. Neurons in the output layer
represent the coordinates of the AUVs and the corresponding
path for each AUV. Each neuron of the output layer is fully con-
nected to the neurons of the input layer. There are K neurons to
establish an optimal path for each AUV, where K ∈ N
+
, so that
there are K × L neurons in all. The connection weight of each
output neuron, i.e., the weight W
jk
=(x, y, z) of that neuron,
is given by a 1 × 3 weight vector, which is initialized as the
coordinates of the initial AUV position. The network is initial-
ized with the weight vector R
jk
= W
jk
=(w
jkx
,w
jky
,w
jkz
),
where j =1, 2,...,J and k =1, 2,...,K. R
jk
changes with
W
jk
during every computation iteration. After the iterations, we
obtain a 3 × J × K matrix R that denotes the coordinates of the
output neurons, i.e., the trajectories of t he AUVs. The input data
set is given sequentially to the network in a random order during
the iterations, i.e., targets’ coordinates are inputted to the net-
work one by one until the last target. This input strategy with the
random order of the input data results in the robustness of the al-
gorithm and reduces its dependence on initial workspace config-
uration. During this process of formation, the visiting sequence
of the points by AUVs is gradually worked out, and the points
would attract output neurons to form a formation for the AUVs.
The iterations end until all of the AUVs reach the points. In
order to assure that each point in the formation gets an AUV, we
set L = J in the algorithm. Note that the relationship between
L and J are defined by the algorithm, which means the corre-
spondence between AUVs and the target points are not fixed.
III. M
AIN ALGORITHM
In order to further explain how the SOM method is applied
on formation control of a multiple AUV system, mathematical
models and formulas with some discussions are given in this
section.
Notations and definitions: for a vector ω ∈ R
n
, the norm |·|
is defined as |ω| = |ω|
2
=(
n
i =1
|ω
i
|
2
)
1
2
.
Authorized licensed use limited to: Southeast University. Downloaded on October 15,2020 at 03:04:21 UTC from IEEE Xplore. Restrictions apply.
剩余10页未读，继续阅读
王莽v2
- 粉丝: 1w+
- 资源: 21
我的内容管理
展开
最新资源
- BGP协议首选值(PrefVal)属性与模拟组网实验
- C#实现VS***单元测试coverage文件转xml工具
- NX二次开发：UF_DRF_ask_weld_symbol函数详解与应用
- 从机FIFO的Verilog代码实现分析
- C语言制作键盘反应力训练游戏源代码
- 简约风格毕业论文答辩演示模板
- Qt6 QML教程：动态创建与销毁对象的示例源码解析
- NX二次开发函数介绍：UF_DRF_count_text_substring
- 获取inspect.exe：Windows桌面元素查看与自动化工具
- C语言开发的大丰收游戏源代码及论文完整展示
- 掌握NX二次开发：UF_DRF_create_3pt_cline_fbolt函数应用指南
- MobaXterm：超越Xshell的远程连接利器
- 创新手绘粉笔效果在毕业答辩中的应用
- 学生管理系统源码压缩包下载
- 深入解析NX二次开发函数UF-DRF-create-3pt-cline-fcir
- LabVIEW用户登录管理程序：注册、密码、登录与安全
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
