算法基础试题解析：递归方程与二项堆操作

"这是一份来自2009-2010学年的算法基础考试试卷，包含了多项选择题和计算题，涉及递归方程的求解、二项堆的操作、最长公共子序列计算、前缀编码以及最小生成树等核心算法概念。" 在这份试卷中，我们可以看到几个关键的算法知识点： 1. **时间复杂度分析**：题目要求证明函数\( f(n) = n^2 \)是\( O(g(n)) \)，其中\( g(n) = n^2 \)。这涉及到大O记法，它是算法分析中用于描述算法运行时间增长速度的一种方式。在这里，显然\( f(n) \)的增长速率与\( g(n) \)相同，因此可以证明\( f(n) \)属于\( O(g(n)) \)。 2. **不匹配的时间复杂度**：题目要求举例说明存在函数\( f(n) \)，使得\( f(n) \neq O(n) \)且\( f(n) \neq \Omega(n) \)。这提示我们需要找到一个函数，它的增长既不线性也不低于线性。例如，可以选择\( f(n) = n\log n \)。这个函数既不是\( O(n) \)也不是\( \Omega(n) \)，因为它的增长速度介于线性与平方之间。 3. **递归方程求解**：两个递归方程被给出，分别是\( T(n) = 8T(\frac{n}{2}) + n \)和\( T(n) = 3T(\frac{n}{3}) + \log_3 n \)。解决这类问题通常采用主定理或画出分治树来分析。对于第一个方程，其时间复杂度是\( O(n) \)，因为每个节点的贡献是\( n \)，而分支因子是8，所以总共的运算次数是\( n \)的对数级别。第二个方程的时间复杂度是\( O(n\log n) \)，因为分支因子为3，而每个节点的贡献是\( \log_3 n \)。 4. **二项堆操作**：二项堆是一种特殊的堆数据结构，用于支持插入和删除最小元素（Extract-Min）等操作。在二项堆中执行Extract-Min，通常涉及将根节点与最后一个孩子交换，然后通过下沉操作维护堆性质，直至找到新的最小元素并返回。 5. **最长公共子序列**：这是动态规划的一个经典应用。给定两个序列X和Y，我们需要找到它们的最长公共子序列，即在不改变顺序的情况下，两个序列共有的最长子串。可以使用二维动态规划表来解决，其中每个单元格表示对应子序列的长度。 6. **前缀编码**：在信息编码中，前缀码是一种无歧义的编码方式，确保没有编码是其他编码的前缀。对于给定字符频次，构建最小生成树（通常是赫夫曼树）可以得到最优的前缀编码，以最小化编码后的电文总长度。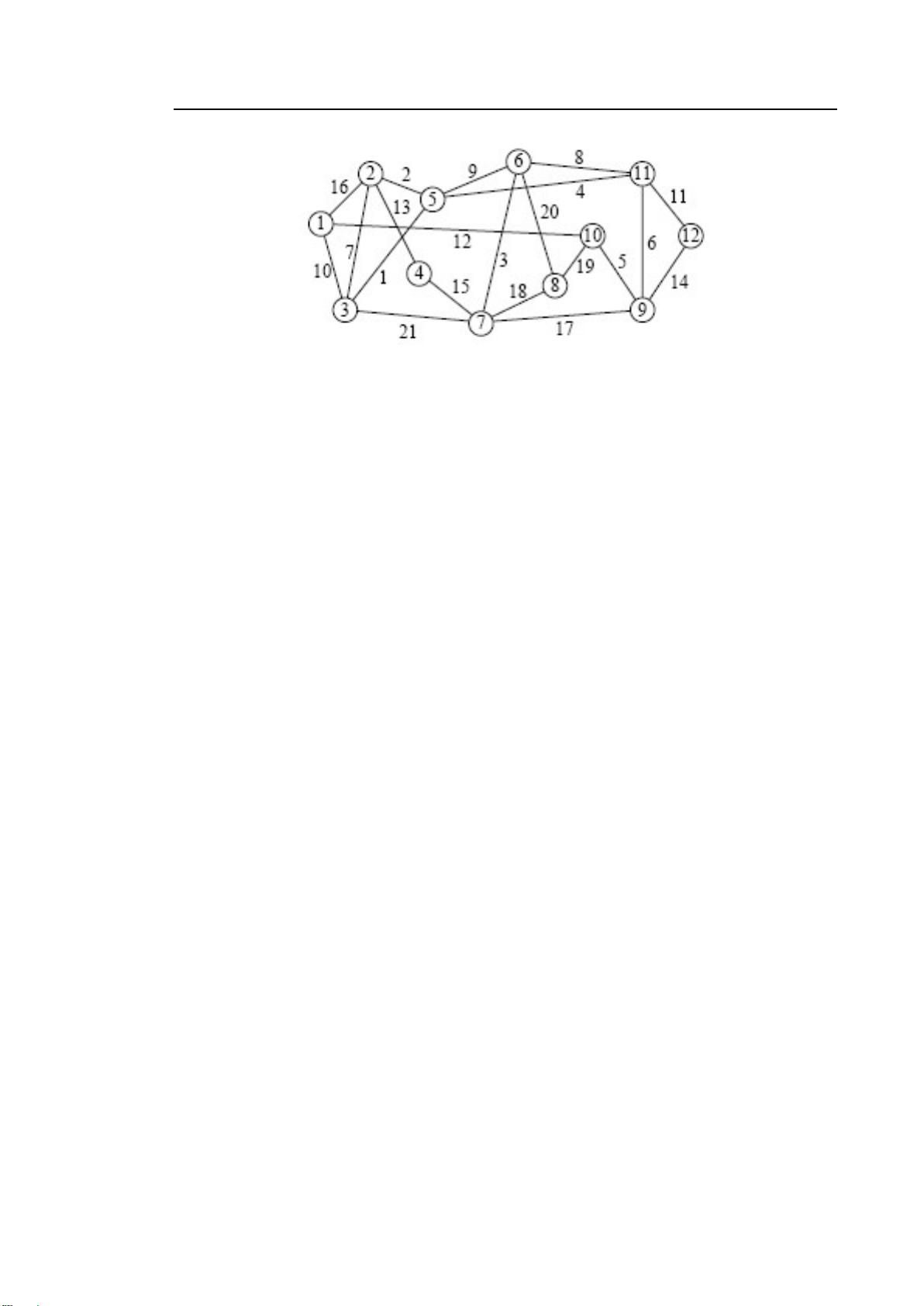 7. **最小生成树**：在带权重的无向图中，找到连接所有顶点的边的集合，使得这些边的总权重最小，这就是最小生成树。常见的算法有Prim算法或Kruskal算法。 8. **算法分析**：最后一部分要求分析给定的算法，如Pesky函数的运行时间和数组Next的操作，这涉及到对循环嵌套深度的理解和运行次数的计算。 这份试卷全面覆盖了算法基础的重要概念，包括时间复杂度分析、递归方程求解、数据结构操作、动态规划、编码理论以及图论中的基本问题，这些都是计算机科学中不可或缺的基础知识。