大规模深度强化学习在Dota 2中的应用

需积分: 13 174 浏览量更新于2024-07-15 收藏 8.4MB PDF 举报

"这篇PDF文档是关于OpenAI团队利用大规模深度强化学习在Dota 2游戏中取得突破的研究。在2019年4月13日，OpenAI Five成为了首个战胜电子竞技游戏Dota 2世界冠军的人工智能系统。Dota 2游戏中的长时间跨度、不完全信息以及复杂连续的状态-动作空间对AI系统提出了新的挑战，这些挑战对于构建更强大的AI系统至关重要。OpenAI Five通过扩展现有的强化学习技术，实现了每两秒大约学习200万个帧的训练速率。他们开发了一套分布式训练系统和持续训练工具，使得OpenAI Five能够连续训练10个月，并最终击败了Dota 2的世界冠军队伍。" 在这篇研究中，OpenAI团队主要关注的是如何运用深度强化学习来解决复杂环境下的策略问题，特别是针对像Dota 2这样的多人在线战斗竞技游戏。深度强化学习是机器学习的一个分支，它结合了深度学习（用于从高维数据中学习抽象特征）与强化学习（通过与环境互动来优化决策策略）。在Dota 2这样的游戏中，AI必须处理大量不确定性和复杂的决策树，这在传统的人工智能方法中是非常困难的。研究中提到的关键点包括： 1. **长时间跨度**：与许多其他游戏相比，Dota 2的比赛时间较长，要求AI具备长期规划和决策能力。这需要一个能够处理长期依赖和延迟奖励的强化学习算法。 2. **不完全信息**：游戏环境中的部分信息是不可见的，AI需要通过推理和观察来推断对手的策略。这需要引入基于概率的模型，如蒙特卡洛树搜索（MCTS）或者部分可观测马尔科夫决策过程（POMDPs）。 3. **复杂连续状态-动作空间**：Dota 2的动作空间巨大且连续，每个英雄有多种可能的动作，AI必须学会在这些动作间做出选择。这需要使用能处理连续动作空间的算法，如策略梯度方法。 4. **大规模并行训练**：OpenAI设计了一个分布式训练系统，能够同时处理大量数据和训练任务，显著加速了学习过程。 5. **持续训练**：OpenAI Five能够持续学习和适应，这可能涉及到在线学习、迁移学习或元学习等技术，以使AI能够从以往的经验中不断改进。通过这些技术的综合应用，OpenAI Five不仅在单个游戏实例上表现出色，而且在长时间的训练后能够适应和对抗不同风格的玩家，展现了深度强化学习在解决复杂、动态问题上的潜力。这一研究对人工智能在游戏、机器人、自动驾驶等领域的应用具有深远的影响。

0 200 400 600 800

100

150

200

250

TrueSkill

Final OpenAI Five TrueSkill = 254

Rerun

OpenAI Five

0 200 400 600 800

Total project compute (PFLOPs/s-days)

100

150

200

250

TrueSkill

15x more

hypothetical always-restart run

time spent retraining from scratch

Figure 4: Training in an environment under development: In the top panel we see the

full history of our project - we used surgery methods to continue training OpenAI Five at each

environment or policy change without loss in performance; then we restarted once at the end to run

Rerun. On the bottom we see the hypothetical alternative, if we had restarted after each change

and waited for the model to reach the same level of skill (assuming pessimistically that the curve

would be identical to OpenAI Five). The ideal option would be to run Rerun-like training from the

very start, but this is impossible — the OpenAI Five curve represents lessons learned that led to

the ﬁnal codebase, environment, etc., without which it would not be possible to train Rerun.

achieve. Learning how to continue long-running training without aﬀecting ﬁnal performance is a

promising area for future work.

Ultimately, while surgery as currently conceived is far from perfect, with proper tooling it

becomes a useful method for incorporating certain changes into long-running experiments without

paying the cost of a restart for each.

4.3 Batch Size

In this section, we evaluate the beneﬁts of increasing the batch size using small scale experiments.

Increasing the batch size in our case means two things: ﬁrst, using twice as many optimizer GPUs

to optimize over the larger batch, and second, using twice as many rollout machines and forward

pass GPUs to produce twice as many samples to feed the increased optimizer pool.

One compelling benchmark to compare against when increasing the batch size is linear speedup:

using 2x as much compute gets to the same skill level in 1/2 the time. If this scaling property

holds, it is possible to use the same total amount of GPU-days (and thus dollars) to reach a given

result[28]. In practice we see less than this ideal speedup, but the speedup from increasing batch

size is still noticeable and allows us to reach the result in less wall time.

To understand how batch size aﬀects training speed, we calculate the “speedup” of an experiment

to reach various TrueSkill thresholds, deﬁned as:

speedup(T ) =

Versions for baseline to ﬁrst reach TrueSkill T

Versions for experiment to ﬁrst reach TrueSkill T

(2)

The results of varying batch size in the early part of training can be seen in Figure 5. Full

details of the experimental setup can be found in Appendix M. We ﬁnd that increasing the batch

size speeds up training through the regime we tested, up to batches of millions of observations.

Using the scale of Rerun, we were able to reach superhuman performance in two months. In

Figure 5a, we see that Rerun’s batch size (983k time steps) had a speedup factor of around 2.5x

over the baseline batch size (123k). If we had instead used the smaller batch size, then, we might

expect to wait 5 months for the same result. We speculate that it would likely be longer, as the

speedup factor of 2.5 applies at TrueSkill 175 early in training, but it appears to increase with higher

TrueSkill.

Per results in [28], we hoped to ﬁnd (in the early part of training) linear speedup from increasing

batch size; i.e. that it would be 2x faster to train an agent to certain thresholds if we use 2x the

compute and data. Our results suggest that speedup is less than linear. However, we speculate

that this may change later in training when the problem becomes more diﬃcult. Also, given the

relevant compute costs, in this ablation study we did not tune hyperparameters such as learning

rate separately for each batch size.

4.4 Data Quality

One unusual feature of our task is the length of the games; each rollout can take up to two hours to

complete. For this reason it is infeasible for us to optimize entirely on fully on-policy trajectories;

if we waited to apply gradient updates for an entire rollout game to be played using the latest

parameters, we could make only one update every two hours. Instead, our rollout workers and

optimizers operate asynchronously: rollout workers download the latest parameters, play a small

0k 2k 5k 7k 10k 12k 15k

Parameter versions

100

125

150

175

200

Trueskill

Batch size 1966k

Batch size 983k

Batch size 492k

Batch size 246k

Batch size 123k (b)

Batch size 61k

61k 123k 246k 492k 983k 1966k

Batch size (in frames, log scale)

0.0

0.5

1.0

1.5

2.0

2.5

3.0

Speedup

TS175

TS125

TS100

Linear speedup

(a) Batch size: Larger batch

size speeds up training. In the

early part of training studied

here, the speedup is sublinear in

the computation and samples re-

quired. See subsection M.1 for ex-

periment details.

0k 2k 4k 6k 8k 10k

Parameter versions

100

125

150

175

200

Trueskill

Queue length 0 (b)

Queue length 1

Queue length 2

Queue length 4

Queue length 8

Queue length 16

Queue length 32

2 4 8 16 32

Measured staleness (log)

0.0

0.2

0.4

0.6

0.8

1.0

1.2

Speedup

TS150

TS125

TS100

(b) Data Staleness: Training

on stale rollout data causes

signiﬁcant losses in training

speed. Queue length estimates

the amount of artiﬁcial staleness

introduced; see subsection M.2

for experiment details.

0k 2k 4k 6k

Parameter versions

100

125

150

175

200

Trueskill

Sample Reuse 0.5

Sample Reuse 1 (b)

Sample Reuse 2

Sample Reuse 4

Sample Reuse 8

0.5 1.0 2.0 4.0 8.0

Measured sample reuse (log)

0.0

0.2

0.4

0.6

0.8

1.0

1.2

Speedup

TS125

TS100

each sample of training data

causes signiﬁcant slowdowns. See

subsection M.3 for experiment de-

tails.

Figure 5: Batch Size and data quality in early training: For each parameter, we ran multiple

training runs varying only that parameter. These runs cover early training (approximately one

week) at small scale (8x smaller than Rerun). On the left we plot TrueSkill over time for each run.

On the right, we plot the “speedup” to reach ﬁxed TrueSkill thresholds of 100, 125, 150, and 175 as a

function of the parameter under study compared to the baseline (marked with ‘b’); see Equation 2.

Higher speedup means that training was faster and more eﬃcient. These four thresholds are chosen

arbitrarily; a few are omitted when the uncertainties are too large (for example in Figure 5c fewer

than half the experiments reach 175, so that speedup curve would not be informative).

portion of the game, and upload data to the experience buﬀer, while optimizers continually sample

from whatever data is present in the experience buﬀer to optimize (Figure 2).

Early on in the project, we had rollout workers collect full episodes before sending it to the

optimizers and downloading new parameters. This means that once the data ﬁnally enters the

optimizers, it can be several hours old, corresponding to thousands of gradient steps. Gradients

computed from these old parameters were often useless or destructive. In the ﬁnal system rollout

workers send data to optimizers after only 256 timesteps, but even so this can be a problem.

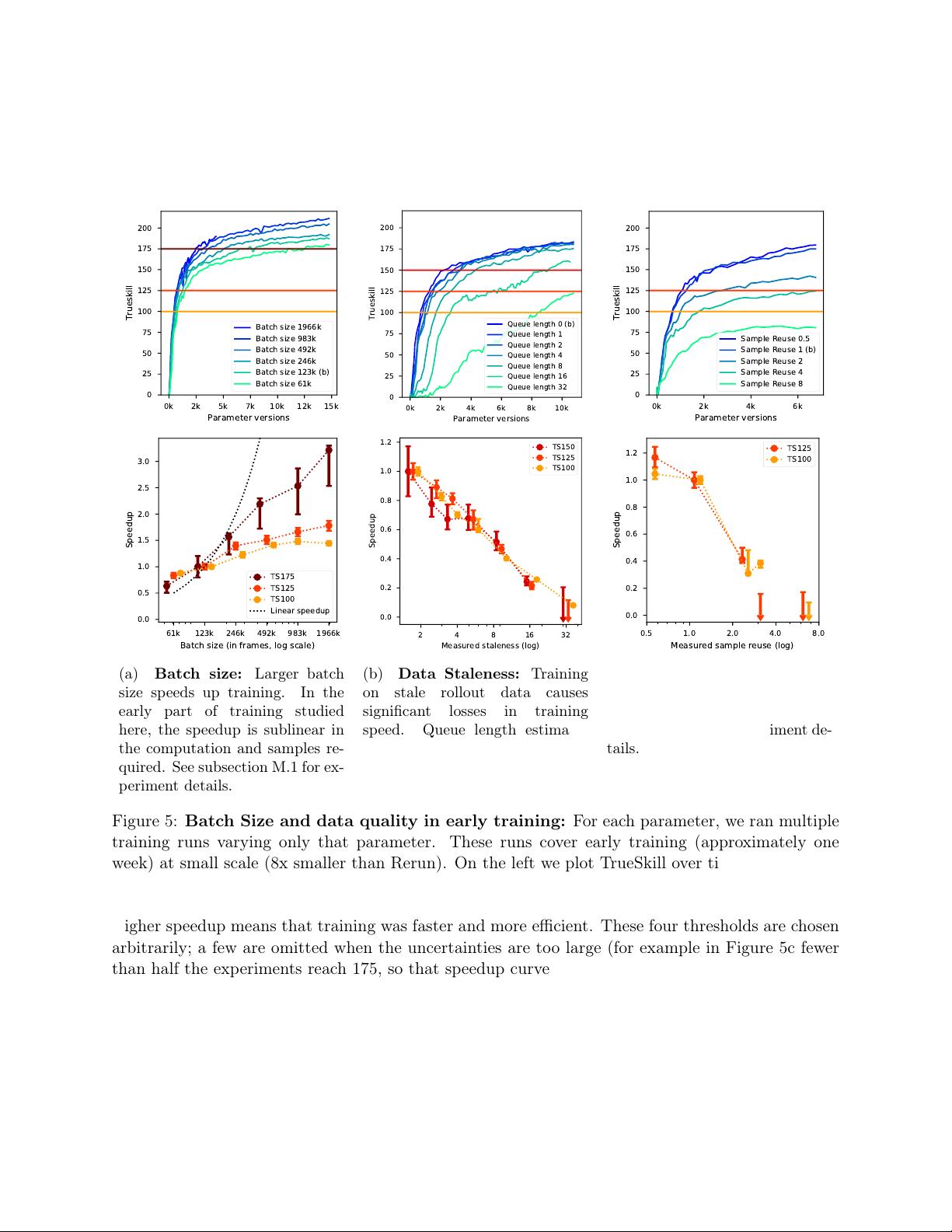
We found it useful to deﬁne a metric for this called staleness. If a sample was generated

by parameter version N and we are now optimizing version M, then we deﬁne the staleness of

that data to be M − N. In Figure 5b, we see that increasing staleness by ∼ 8 versions causes

signiﬁcant slowdowns. Note that this level of staleness corresponds to a few minutes in a multi-

month experiment. Our ﬁnal system design targeted a staleness between 0 and 1 by sending game

data every 30 seconds of gameplay and updating to fresh parameters approximately once a minute,

making the loop faster than the time it takes the optimizers to process a single batch (32 PPO

gradient steps). Because of the high impact of staleness, in future work it may be worth investigating

whether optimization methods more robust to oﬀ-policy data could provide signiﬁcant improvement

in our asynchronous data collection regime.

Because optimizers sample from an experience buﬀer, the same piece of data can be re-used many

times. If data is reused too often, it can lead to overﬁtting on the reused data[18]. To diagnose this,

we deﬁned a metric called the sample reuse of the experiment as the instantaneous ratio between

the rate of optimizers consuming data and rollouts producing data. If optimizers are consuming

samples twice as fast as rollouts are producing them, then on average each sample is being used

twice and we say that the sample reuse is 2. In Figure 5c, we see that reusing the same data even

2-3 times can cause a factor of two slowdown, and reusing it 8 times may prevent the learning of a

competent policy altogether. Our ﬁnal system targets sample reuse ∼ 1 in all our experiments.

These experiments on the early part of training indicate that high quality data matters even

more than compute consumed; small degradations in data quality have severe eﬀects on learning.

Full details of the experiment setup can be found in Appendix M.

4.5 Long term credit assignment

Dota 2 has extremely long time dependencies. Where many reinforcement learning environment

episodes last hundreds of steps ([4, 29–31]), games of Dota 2 can last for tens of thousands of time

steps. Agents must execute plans that play out over many minutes, corresponding to thousands of

timesteps. This makes our experiment a unique platform to test the ability of these algorithms to

understand long-term credit assignment.

In Figure 6, we study the time horizon over which our agent discounts rewards, deﬁned as

H =

1 − γ

(3)

Here γ is the discount factor [17] and T is the real game time corresponding to each step (0.133

seconds). This measures the game time over which future rewards are integrated, and we use it as

a proxy for the long-term credit assignment which the agent can perform.

In Figure 6, we see that resuming training a skilled agent using a longer horizon makes it perform

better, up to the longest horizons we explored (6-12 minutes). This implies that our optimization

was capable of accurately assigning credit over long time scales, and capable of learning policies and

剩余65页未读，继续阅读

星桥翊月

粉丝: 1
资源: 7

大规模深度强化学习在Dota 2中的应用

深度强化学习精要：Grokking Deep Reinforcement Learning

"深度学习：自适应计算与机器学习经典指南

"神经网络与深度学习绪论及课程概要详解

Continuous control with deep reinforcement learning.pdf

placement optimization with deep reinforcement learning.pdf

DDPG-Continuous Control with Deep Reinforcement Learning.pdf

Towards Playing Full MOBA Games withDeep Reinforcement Learning.pdf

An Introduction to Deep Reinforcement Learning.pdf

A brief Survey of Deep Reinforcement Learning.pdf

Human-level control through deep reinforcement learning.pdf

最新资源