Matlab基础：数值积分方法及应用详解

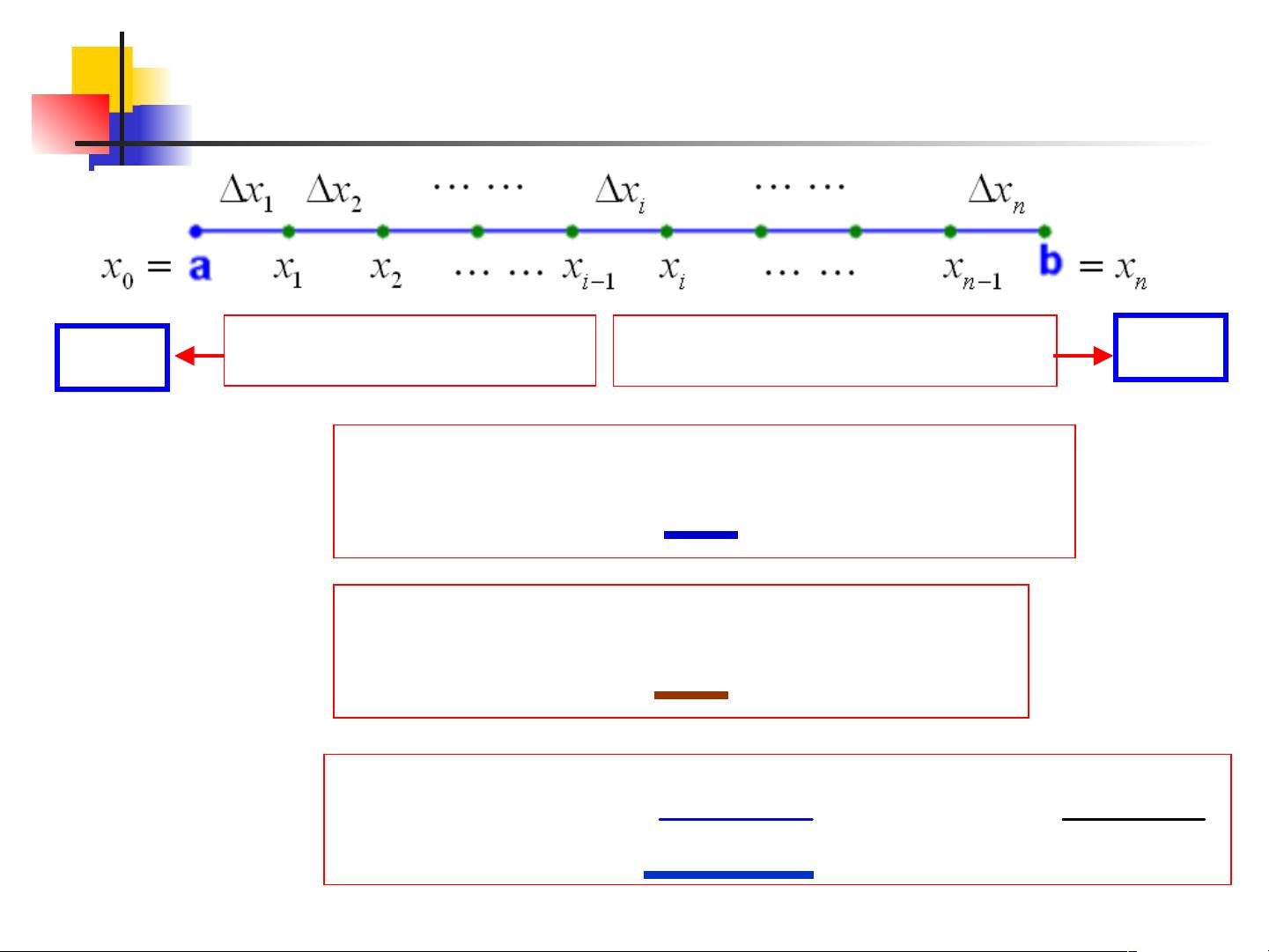
本节主要介绍了 Matlab 中关于数值积分的基础知识和相关函数。在数值积分中，定积分的近似计算是一项重要的任务。当被积函数的原函数不知道时，或者只有离散的采样值时，我们需要利用近似方法来计算定积分。在本节中，主要讨论了定积分的三种近似计算算法：矩形法、梯形法和抛物线法，并介绍了 Matlab 中用于计算定积分的相关函数。 首先，在矩形法中，定积分的近似计算可以通过将区间划分为若干子区间，并在每个子区间中取一个采样点来计算被积函数的平均值。这样可以得到定积分的近似值。在 Matlab 中，可以使用 sum(a) 函数来计算数组 a 的和，同时还可以使用 format long 函数来设置屏幕显示的有效数字位数，以及使用 trapz() 函数来进行梯形法的数值积分计算。 其次，梯形法是定积分的一种近似计算方法，通过将每个子区间近似成一个梯形，然后计算每个梯形的面积之和来近似定积分的值。在 Matlab 中，可以使用 trapz() 函数来实现梯形法的数值积分计算。另外，还介绍了 quad() 函数用于抛物线法的数值积分计算，以及 dblquad() 函数用于抛物线法求二重数值积分。 最后，本节还介绍了如何使用 fprintf 函数将数据写入指定的文件中。在实际应用中，有时候被积函数没有解析表达式，而只有一组离散的采样值，这时只能通过近似计算方法来求解定积分。通过掌握 Matlab 中数值积分的相关函数和算法，可以更加方便地进行定积分的数值计算，并解决实际问题中的数值积分计算需求。 综上所述，本节主要介绍了 Matlab 中的数值积分基础知识和相关函数，包括矩形法、梯形法、抛物线法等定积分的近似计算方法，并通过具体的代码示例和应用场景，帮助读者更好地理解和应用数值积分计算的相关知识。通过学习本节内容，读者可以更加熟练地运用 Matlab 中的数值积分工具，解决实际问题中的定积分计算需求。