MATLAB教学：傅里叶变换与频域滤波解析

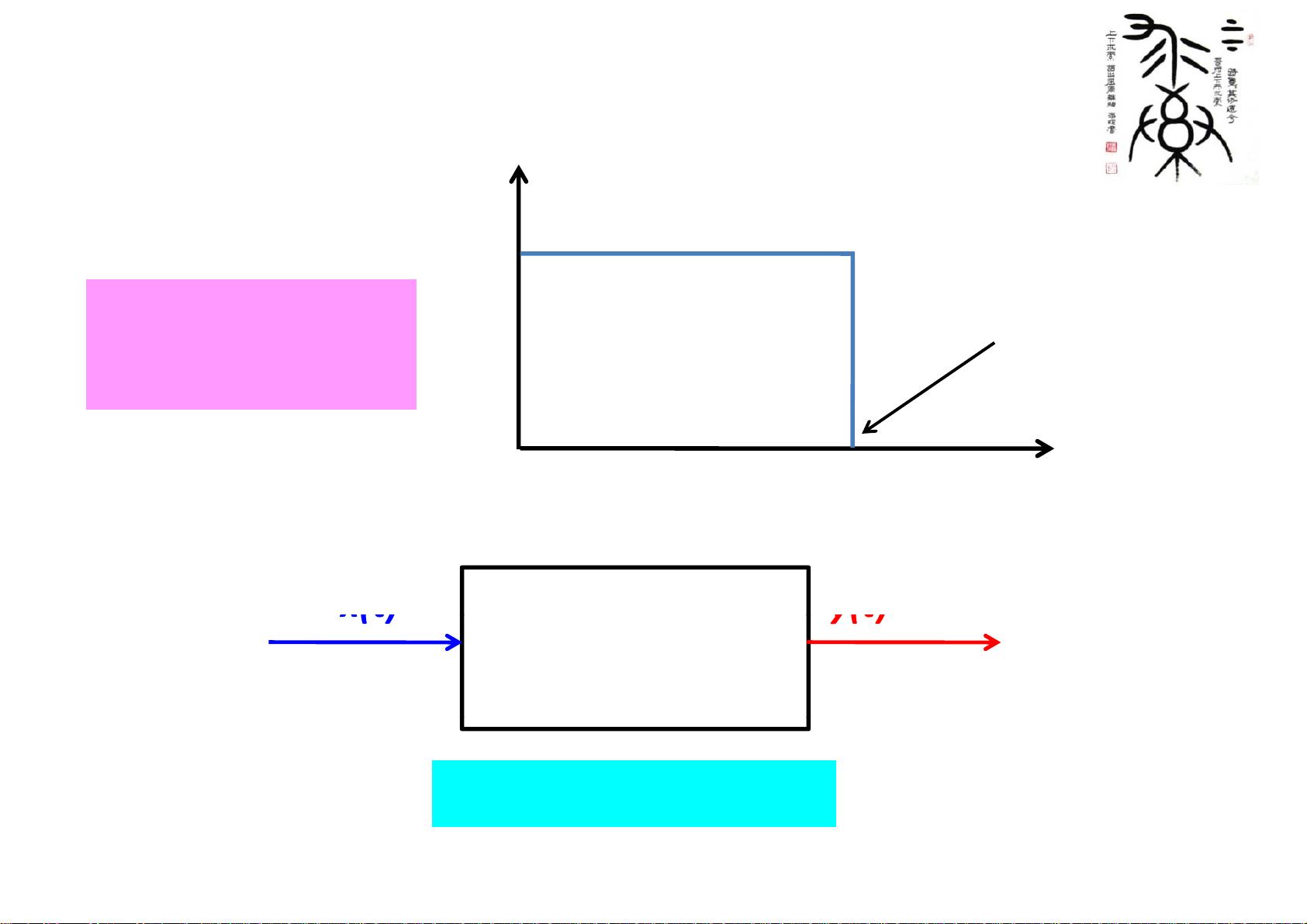
"MATLAB教学视频，讲解傅里叶变换在频域滤波中的应用，涉及理想低通滤波器和RC滤波器" 本教学视频深入解析了MATLAB中傅里叶变换在处理信号滤波问题上的应用。傅里叶变换是将时域信号转化为频域信号的关键工具，它能帮助我们分析信号的频率成分。视频首先介绍了系统对输入信号的稳态响应概念，以输入信号x(t)为例，解释了如何通过傅里叶变换将其转化为频域表示X(jω)。 系统对输入信号的响应取决于系统的频率响应H(jω)。当输入信号X(jω)与系统频率响应H(jω)相乘后，得到输出信号的频域表示Y(jω)，然后通过傅里叶逆变换恢复到时域信号y(t)。这一过程可以用以下数学关系表示：Y(jω) = X(jω) * H(jω)，再对Y(jω)进行傅里叶逆变换得到y(t)。 视频中还具体讨论了两种滤波器：理想低通滤波器和RC滤波器。理想低通滤波器的频率响应H(jω)在截止频率fc以下为1，以上为0，它能有效地保留低频成分，去除高频噪声。当信号x(t)通过理想低通滤波器时，其高于截止频率的频率分量会被完全消除，只保留低频部分，从而实现滤波效果。 另一方面，RC低通滤波器和RC高通滤波器则利用RC电路的特性来实现滤波。RC低通滤波器允许低频信号通过，而衰减高频信号；RC高通滤波器则相反，它允许高频信号通过，而衰减低频信号。这些滤波器在实际信号处理中有着广泛的应用，例如在音频处理、图像处理和通信系统中。 视频还给出了一个示例，其中包含三个不同频率的余弦信号（f1=5Hz，f2=70Hz，f3=200Hz），并假设信号是以1000Hz的采样频率采集的。通过这些滤波器，我们可以选择性地保留或去除特定频率的信号成分，这对于信号分析和噪声抑制至关重要。 这个MATLAB教学视频深入浅出地讲解了傅里叶变换在频域滤波中的应用，对于理解数字信号处理和滤波器设计的基础知识非常有帮助。无论是初学者还是有一定经验的工程师，都能从中受益，提升自己的MATLAB技能和频域滤波理论理解。