数据挖掘实战：线性回归详解与应用

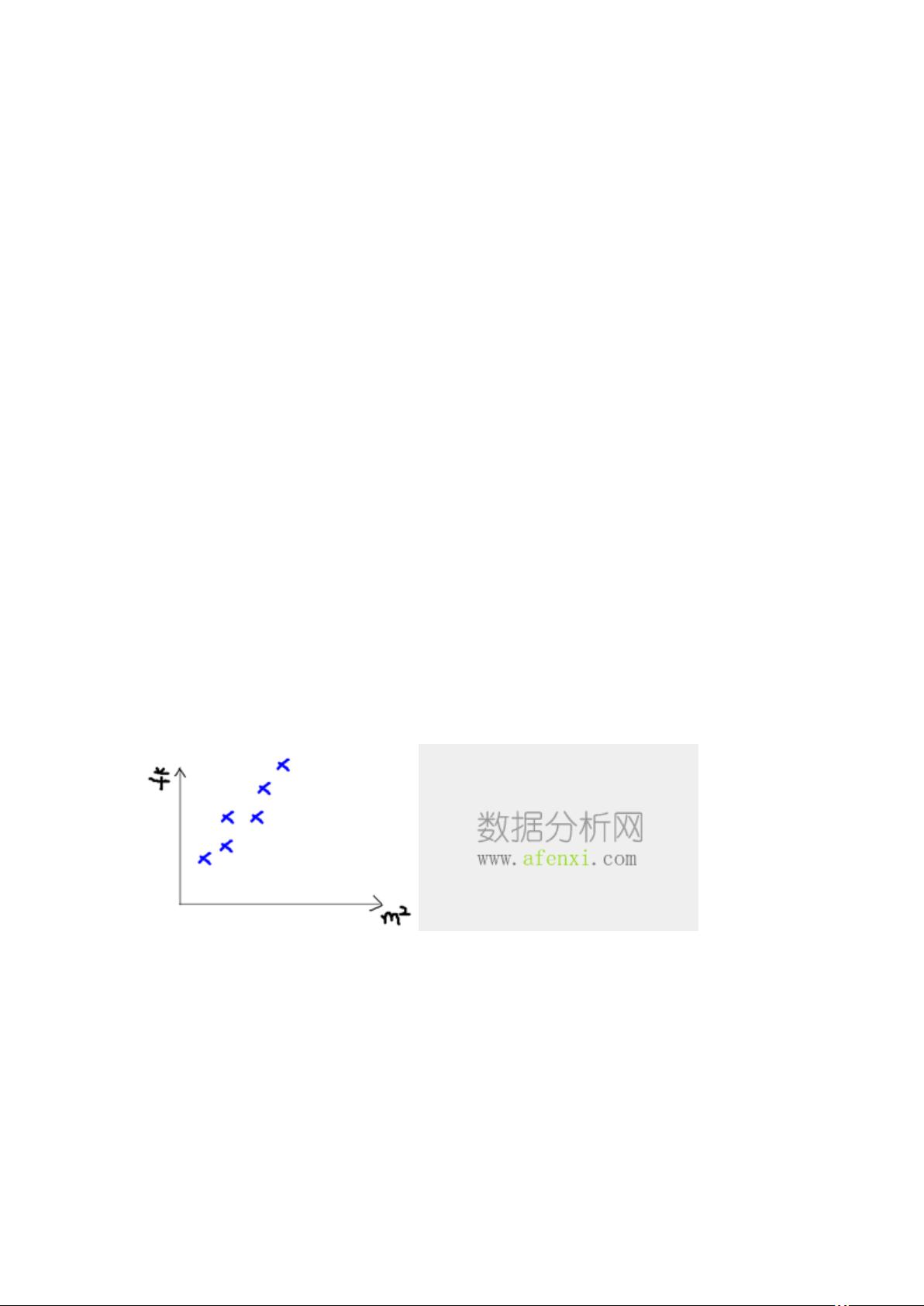
线性回归是数据挖掘中的核心技术之一，它属于回归分析的一种，主要用于研究和理解自变量与因变量之间的线性关系。在统计建模中，线性回归模型基于最小二乘法原理，通过找到一条直线或超平面来最优化地拟合数据，使得实际观测值与预测值之间的误差平方和最小。 在实际应用中，例如房价预测，线性回归可以帮助我们分析房屋面积和售价之间的关系。在这个案例中，数据集包含房屋的面积作为自变量（X），销售价格作为因变量（Y）。通过收集的数据点，可以构建一个一元线性回归模型（单个自变量的情况）或多元线性回归模型（涉及多个自变量）。一元线性回归通过一条直线来表达关系，而多元线性回归则适用于更复杂的多变量关联分析。 在机器学习流程中，数据集通常分为训练集和测试集。训练集用于训练模型，即通过调整回归系数来找到最佳拟合直线，而测试集则是验证模型性能和泛化能力的关键。输入数据（特征向量）的维度，即特征的数量（n），对模型的复杂性和解释性有很大影响。对于新的未知数据点，一旦模型训练完成，可以通过输入其面积值，计算出对应的最佳预测售价。 线性回归的模型通常表示为y = h(x)，其中h(x)是预测函数，x是输入变量的值。回归系数（也称权重）是模型参数，它们通过最小化残差平方和（RSS）来确定，这是衡量实际值与预测值差异的一个度量。在实际应用时，可能需要进行特征缩放、特征选择或正则化等预处理步骤，以提高模型的稳定性和防止过拟合。 线性回归具有计算效率高、模型易于理解和解释的优点，但其假设输入和输出之间的关系是线性的，如果数据分布不满足这个假设，可能需要采用非线性回归或其他更复杂的模型。线性回归是数据挖掘领域中的基础工具，为许多实际问题提供了强大的预测能力。