二元查找树转双向链表的巧妙递归解法

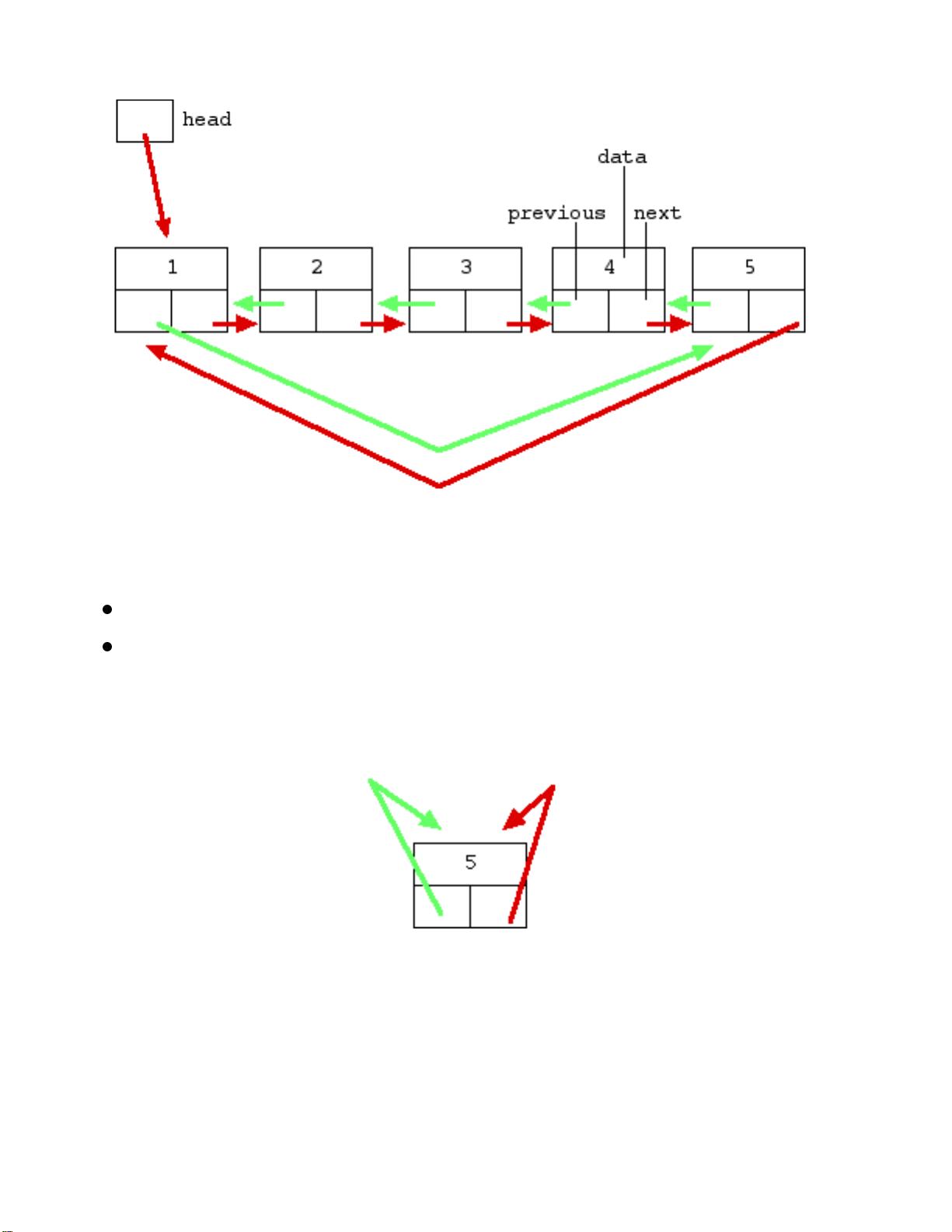
本文档探讨的是将二元查找树（Binary Search Tree, BST）转换为双向链表（Doubly Linked List, DLL）的问题，这是一项高级的编程挑战，涉及到了指针、数据结构、递归算法以及两种数据结构的深入理解。作者尼克·帕拉兰特（Nick Parlante）基于斯坦福大学计算机科学教育图书馆（Stanford CSEducation Library）的文档，提供了一个问题陈述、详细的解释图解以及用Java和C语言的示例代码。 在文章的开头，我们首先了解到了二元查找树的概念，它是一种特殊的二叉树，其中每个节点的左子树中的所有节点值都小于该节点的值，而右子树中的所有节点值都大于该节点的值。这样，对于每个节点，我们可以快速地通过比较来查找、插入或删除元素，因为它保持了元素的有序性。 接下来，文章引入了双向链表，这是一种具有前后两个指针的链表，可以方便地在链表的两端进行插入和删除操作。双向链表的特点是每个节点都有前一个节点和后一个节点的引用，这使得遍历和操作更加灵活。 "挑战"部分是文章的核心，它要求我们设计一个递归算法，将二元查找树转换成一个循环的双向链表。在这个过程中，关键在于处理递归的终止条件、遍历过程中的节点连接以及如何保持原有的树形结构的有序性。递归策略可能包括将当前节点的左子树转换为链表，然后将当前节点链接到链表的末尾，最后处理右子树。 解决此问题时，我们需要利用递归函数，将问题分解为更小的子问题，例如先处理左子树，再处理当前节点，最后处理右子树。在每次递归调用中，都需要更新前驱和后继指针，确保链表结构的正确性。此外，由于目标是形成循环链表，所以在递归结束时需要特别处理根节点，使其指向最后一个节点，从而形成闭环。 作者提供了Java和C语言的示例代码，这些代码可以帮助读者理解问题的解决思路，包括如何使用节点类、递归函数以及如何维护链表和树的对应关系。通过阅读这篇文档，读者不仅能掌握将二元查找树转化为双向链表的方法，还能提升对数据结构和递归算法的熟练运用能力。 此外，文档还提及了与本文相关的其他资源，如“基础的链表”（LinkedList Basics, #103）、链表问题（LinkedList Problems, #105）和二叉树基础（Binary Trees, #110），进一步丰富了读者在数据结构学习路径上的选择。这篇文章是一次深入探究复杂数据结构转换技巧的宝贵学习机会。