傅立叶变换与图像处理探索：从正交变换到小波变换的应用

"该资源是一份关于数字图像处理的经典题目解答，包含了操作步骤和Matlab源码。讨论了正交变换的共同特点及其在图像处理中的应用，特别提到了傅里叶变换和平移，以及小波变换的主要用途，并提供了一个实际的图像处理示例，涉及对'moon.tif'图像进行傅里叶变换以及对另一图像进行小波变换的操作。" 在图像处理领域，正交变换起着至关重要的作用。它们主要包括傅里叶变换、离散余弦变换、沃尔什变换和哈尔变换等。这些变换有以下共同特点： 1. **空域到频域的转化**：它们都通过一组正交基函数将图像从空域转换到频域，揭示图像的频率成分。 2. **唯一对应**：空域的复函数与频域的复函数之间存在唯一的对应关系，保证了可逆性。 3. **保持奇偶性**：变换过程中保持原函数的奇偶性不变。 4. **可逆过程**：正交变换可以被逆转，即可以通过逆变换从频域回到空域。 5. **简化处理**：复杂信号的处理在频域往往比空域更为简便。 正交变换在图像处理中的应用广泛： - **边缘检测**：通过保留高频分量，可以突出图像的边缘，从而实现边缘检测。 - **图像恢复**：基于图像退化模型，可以在频域内恢复或重建原始图像。 - **图像重建**：利用傅里叶变换的旋转性质，可以对图像进行角度校正或重建。 - **图像压缩**：如离散余弦变换，通过傅里叶系数直接压缩图像数据。 - **图像去噪**：使用低通滤波器滤除高频噪声，以达到去除图像噪声的目的。 - **图像分析**：傅里叶描述子可用于区域边界的描述，而傅里叶频谱则能揭示纹理的周期性特征。 在Matlab中，对图像'moon.tif'进行傅里叶变换和平移到中心点的操作如下： 1. 读取图像并转换为灰度格式：`I=imread('moon.tif'); D=double(I)/255;` 2. 执行二维傅里叶变换：`F=fft2(D);` 3. 使用`fftshift`函数将变换结果的原点平移到中心：`Y=fftshift(F);` 4. 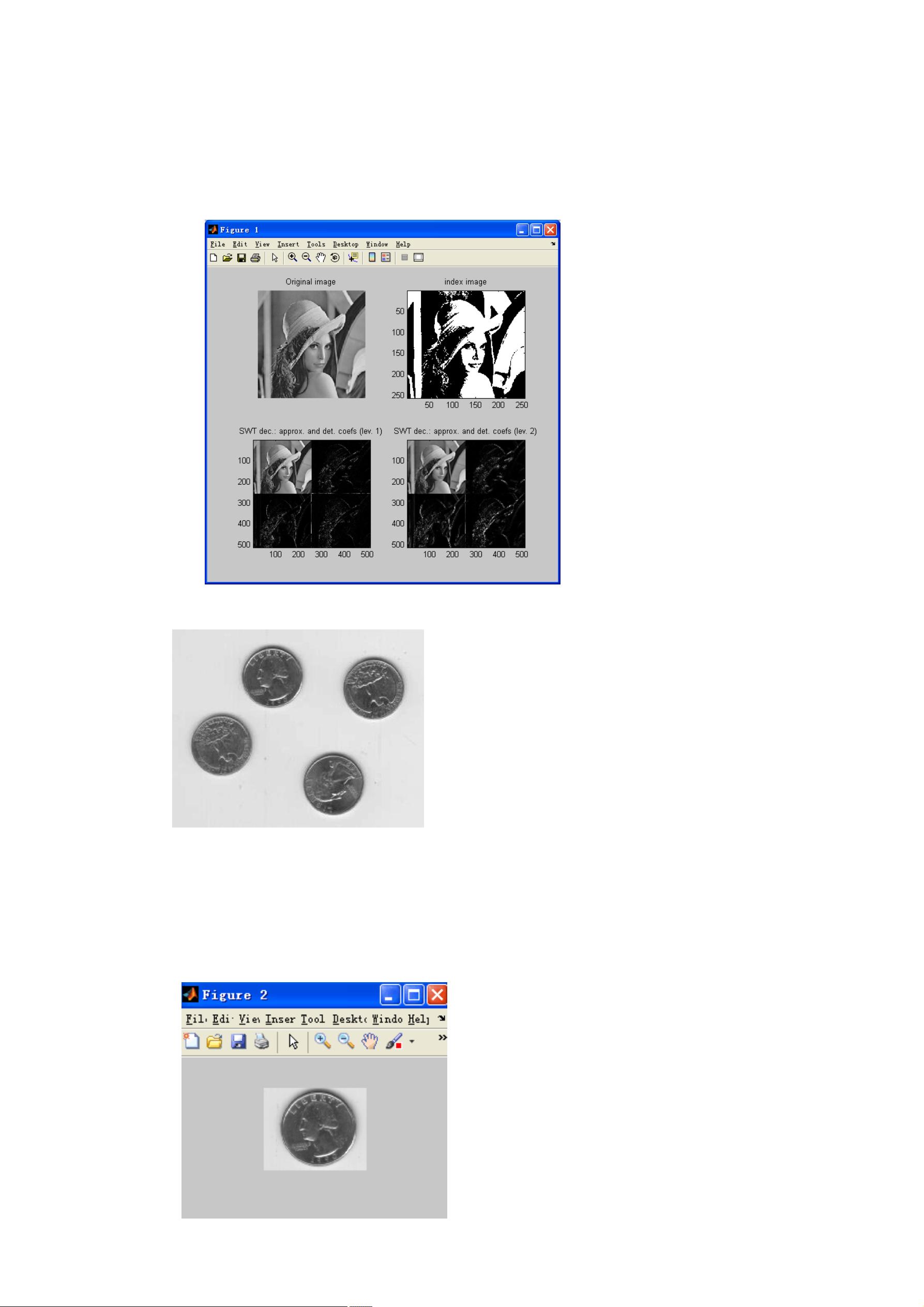显示平移后的频谱：`figure, imshow(Y);` 小波变换是另一种强大的图像处理工具，其主要用途包括： - **多尺度分析**：它能在不同尺度和位置上分析图像，特别适合于处理非平稳信号。 - **细节提取**：小波变换可以分离出图像的局部特征和细节信息。 - **图像去噪**：通过选择合适的小波基，可以有效地去除图像中的噪声，同时保护图像细节。 - **图像压缩**：小波系数的稀疏性有助于实现高效的图像压缩。 - **故障诊断**：在工业领域，小波变换常用于检测设备的异常或故障。 在Matlab中，对图像进行二维小波变换可以使用`swt2`函数，如：`SWC=swt2(X, N, 'wname')`，其中`X`是输入图像，`N`是分解层数，`'wname'`是小波基的名字。 正交变换和小波变换是数字图像处理中的关键技术，它们提供了解析图像、处理噪声、压缩数据和恢复图像的有效手段。通过Matlab这样的工具，我们可以直观地理解和应用这些理论，实现各种图像处理任务。