B树详解：B-Tree、B+Tree与红黑树数据结构

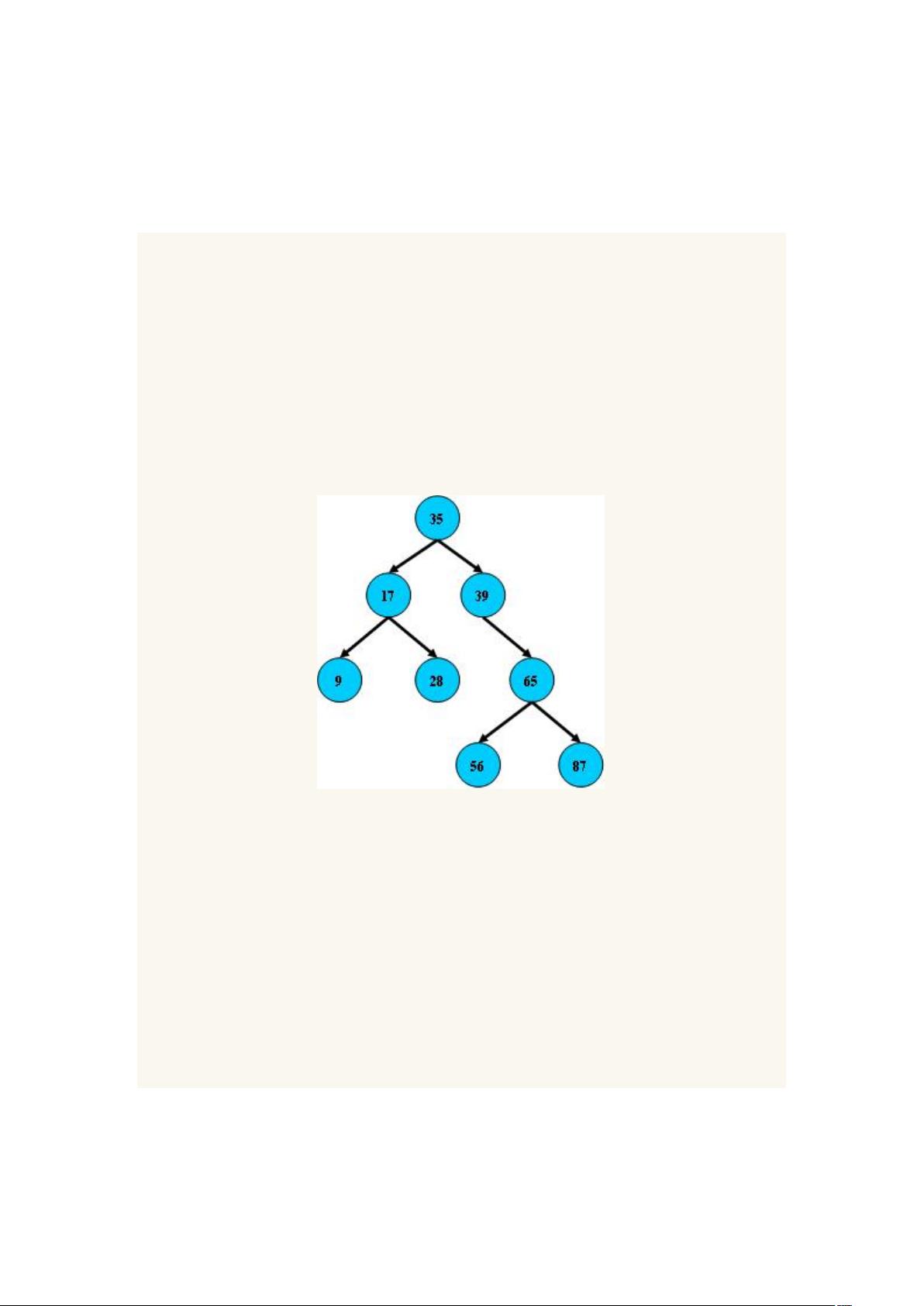
"这篇资源主要介绍了B树、B-Tree数据结构的基础知识，以及它们在索引中的应用。讨论了B树的特性，包括它的平衡性对于搜索性能的影响，以及如何通过平衡算法来维持结构的平衡。同时，还提到了B-Tree的特点，如多路搜索、结点关键字数量的限制等。" 在数据库和文件系统中，索引是一种高效的数据检索方法，B树（Binary Search Tree）和B-Tree（B-Tree）是常见的索引结构。B树是一种自平衡的二叉搜索树，它具有以下关键特点： 1. 每个节点最多有两个子节点，左子节点的值小于当前节点，右子节点的值大于当前节点。 2. 节点存储一个关键字，用于比较和搜索。 3. 插入和删除操作时，通过旋转和复制节点来保持树的平衡，避免了大量数据的移动。 B-Tree则是一种多路搜索树，区别于二叉树，它可以有超过两个子节点，这使得它在处理大数据量时更为高效。B-Tree的主要特征包括： 1. 每个非叶节点最多有M个子节点，M大于2。 2. 根节点的子节点数在[2, M]之间。 3. 非根节点的子节点数在[M/2, M]之间。 4. 每个节点至少包含M/2-1（向上取整）到M-1个关键字。 5. 关键字数量等于子节点数量减一，形成一个有序的序列。 6. 指针P[i]指向关键字K[i]和K[i+1]之间的子树。 B-Tree的搜索过程是从根节点开始，根据关键字序列进行二分查找，如果找到匹配的关键字则结束，否则继续在相应子树中查找。所有叶节点都在同一层级，确保所有查找最终都会终止。 B-Tree的平衡性对于保持搜索效率至关重要。当树失去平衡时，搜索性能会退化为线性，因此需要通过特定的平衡算法来调整结构。这些平衡算法通常在插入和删除节点时执行，确保树的形状尽量接近理想状态，避免出现深度过大或过小的分支。 B树和B-Tree是高效的数据索引工具，尤其适用于大型数据库和文件系统，因为它们能够减少磁盘I/O操作，提高数据检索速度。理解和掌握这些数据结构的原理和操作方式对于优化数据库性能和设计高效的数据存储解决方案至关重要。