优化空间滤波器提升EEG单次试验分析鲁棒性
需积分: 9 148 浏览量
更新于2024-09-04
收藏 1.45MB PDF 举报
本文档《Optimizing Spatial Filters for Robust EEG Single-Trial Analysis》发表于2008年的IEEE SIGNAL PROCESSING MAGAZINE，主要关注电生理信号处理领域，尤其是事件相关电位（Event-Related Potential, ERP）分析中的常见方法——共同空间模式（Common Spatial Pattern, CSP）。CSP是一种在脑机接口（Brain-Computer Interface, BCI）研究中广泛应用的统计方法，其目标是通过优化空间滤波器来提高单次试验（single trial）下信号与噪声比（Signal-to-Noise Ratio, SNR），从而增强神经活动识别的准确性。
CSP的核心原理基于对多通道脑电图（Electroencephalogram, EEG）信号的空间特征进行分离。传统的滤波器设计通常依赖于传感器阵列的几何特性，如拉普拉斯滤波器。然而，CSP算法突破了这种限制，它允许针对每个个体的数据进行自适应滤波器优化，这在处理个体差异显著的脑电信号时具有显著优势。
本文详细阐述了CSP算法的理论基础，包括如何通过计算不同频率或事件类型下的正交特征向量来区分信号源。作者讨论了CSP的不同变体，强调了技术细节和实践经验，例如如何选择合适的基向量数量、如何处理共线性问题，以及如何进行平稳化处理，以减少噪声影响。
此外，文章还介绍了CSP在作者的柏林大脑-机器界面（Berlin Brain-Computer Interface, Berlin BCI）研究中的应用，展示了如何利用CSP预处理技术提升脑电信号的质量，从而改善BCI系统的性能。通过实例，读者可以了解到CSP的实际操作步骤和优化策略，这对于从事相关领域的研究人员来说，是一份宝贵的学习和实践参考资料。该论文对于理解和优化CSP算法在实际应用中的效果具有重要的指导意义。
OPTIMIZING SPATIAL FILTERS FOR ROBUST EEG SINGLE-TRIAL ANALYSIS 3
central
sulcus
motor
sensory
O
P
T
F
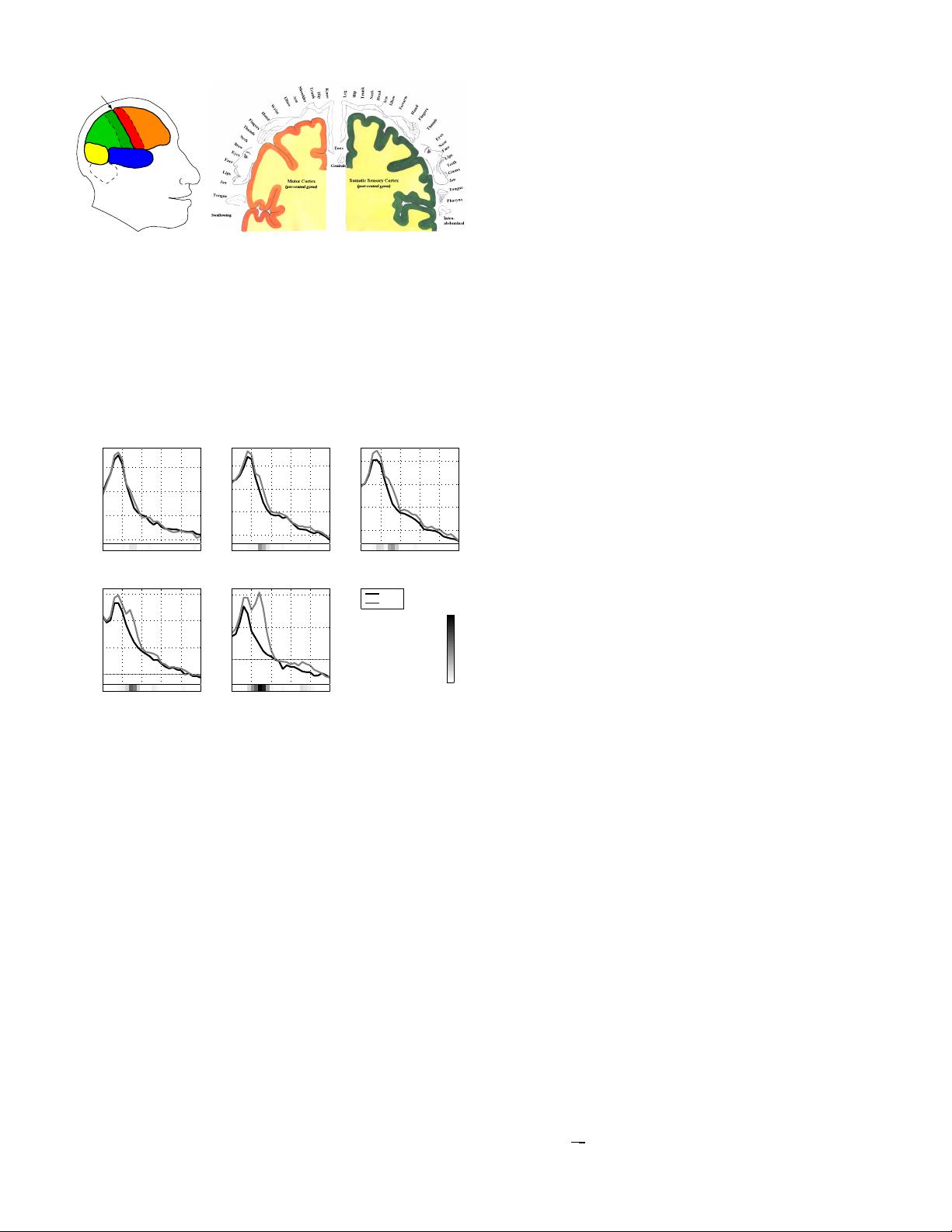
Fig. 3. Left. Lobes of the brain: Frontal, Parietal, Occipital,
and Temporal (named after the bones of the skull beneath which
they are located). The central sulcus separates the frontal and
parietal lobe. Right. Geometric mapping between body parts and
motor/somatosensory cortex. The motor cortex and the somatosensory
cortex are shown at the left and right part of the figure, respectively.
Note, that in each hemisphere there is one motor area (frontal to the
central sulcus) and one sensori area (posterior to the central sulcus).
The part which is not shown can be obtained by mirroring the figure
folded at the center.
5 10 15 20 25 30
15
20
25
30
[Hz]
[dB]
raw: CP4
5 10 15 20 25 30
10
15
20
25
[Hz]
[dB]
bipolar: FC4−CP4
5 10 15 20 25 30
10
15
20
25
[Hz]
[dB]
CAR: CP4
5 10 15 20 25 30
0
5
10
15
[Hz]
[dB]
Laplace: CP4
5 10 15 20 25 30
0
5
10
[Hz]
[dB]
CSP
left
right
0
0.2
0.4
0.6
r
2
Fig. 4. Spectra of left vs. right hand motor imagery. All plots are
calculated from the same dataset but using different spatial filters.
The discrimination between the two conditions is quantified by the
r
2
-value. CAR stands for common average reference.
to the specific characteristics of each user ([19], [2], [7]). For
the latter data-driven approaches to calculate subject-specific
spatial filters have proven to be useful.
As a demonstration of the importance of spatial filters, Fig. 4
shows spectra of left vs. right hand motor imagery at the right
hemispherical sensorimotor cortex. All plots are computed
from the same data but using different spatial filters. While
the raw channel only shows a peak around 9 Hz that provides
almost no discrimination between the two conditions, the
bipolar and the common average reference filter can improve
the discrimination slightly. However the Laplace filter and even
more the CSP filter reveal a second spectral peak around 12 Hz
with strong discriminative power. By further investigations
the spatial origin of the non-discriminative peak could be
traced back to the visual cortex, while the discriminative
peak originates from sensorimotor rhythms. Note that in many
subjects the frequency ranges of visual and sensorimotor
rhythms overlap or completely coincide.
III. METHODS
A. General framework
Here we overview the classifier we use. Let X ∈ R
C×T
be a short segment of EEG signal
2
, which corresponds to a
trial of imaginary movement; C is the number of channels
and T is the number of sampled time points in a trial. A
classifier is a function that predicts the label of a given trial
X. For simplicity let us focus on the binary classification
e.g., classification between imagined movement of left and
right hand. The classifier outputs a real value whose sign is
interpreted as the predicted class. The classifier is written as
follows:
f (X; {w
j
}
J
j=1
, {β
j
}
J
j=0
) =
J
∑
j=1
β
j
log
w
>
j
XX
>
w
j
+ β
0
. (2)
The classifier first projects the signal by J spatial filters
{w
j
}
J
j=1
∈ R
C×J
; next it takes the logarithm of the power of
the projected signal; finally it linearly combines these J di-
mensional features and adds a bias β
0
. In fact, each projection
captures different spatial localization; the modulation of the
rhythmic activity is captured by the log-power of the band-pass
filtered signal. Note that various extensions are possible (see
Sec. V-D). A different experimental paradigm might require
the use of nonlinear methods of feature extraction and classifi-
cation respectively [33]. Direct minimization of discriminative
criterion [17] and marginalization of the classifier weight [22]
are suggested. On the other hand, methods that are linear in
the second order statistics X X
>
, i.e., Eq. (2) without the log,
are discussed in [49], [48] and shown to have some good
properties such as convexity.
The coefficients {w
j
}
J
j=1
and {β
j
}
J
j=1
are automatically
determined statistically ([21]) from the training examples i.e.,
the pairs of trials and labels {X
i
,y
i
}
n
i=1
we collect in the
calibration phase; the label y ∈ {+1,−1} corresponds to, e.g.,
imaginary movement of left and right hand, respectively, and
n is the number of trials.
We use Common Spatial Pattern (CSP) [18], [27] to deter-
mine the spatial filter coefficients {w
j
}
J
j=1
. In the following,
we discuss the method in detail and present some recent
extensions. The linear weights {β
j
}
J
j=1
are determined by
Fisher’s linear discriminant analysis (LDA).
B. Introduction to Common Spatial Patterns Analysis
Common Spatial Pattern ([18], [27]) is a technique to
analyze multi-channel data based on recordings from two
classes (conditions). CSP yields a data-driven supervised de-
composition of the signal parameterized by a matrix W ∈R
C×C
(C being the number of channels) that projects the signal
x(t) ∈ R
C
in the original sensor space to x
CSP
(t) ∈ R
C
, which
lives in the surrogate sensor space, as follows:
x
CSP
(t) = W
>
x(t).
2
In the following, we also use the notation x(t) ∈R
C
to denote EEG signal
at a specific time point t; thus X is a column concatenation of x(t)’s as
X = [x(t),x(t +1), . . .,x(t + T −1)] for some t but the time index t is omitted.
For simplicity we assume that X is already band-pass filtered, centered and
scaled i.e., X =
1
√
T
X
band−pass
(I
T
−1
T
1
>
T
), where I
T
denotes T ×T identity
matrix and 1
T
denotes a T-dimensional vector with all one.
剩余11页未读，继续阅读
2023-02-28 上传
2024-06-13 上传
2013-06-05 上传
2019-10-23 上传
2022-01-21 上传
2020-09-22 上传
2021-06-26 上传
2019-09-27 上传
2017-09-10 上传
zhoudapeng01
- 粉丝: 277
- 资源: 33
我的内容管理
展开
最新资源
- 黑板风格计算机毕业答辩PPT模板下载
- CodeSandbox实现ListView快速创建指南
- Node.js脚本实现WXR文件到Postgres数据库帖子导入
- 清新简约创意三角毕业论文答辩PPT模板
- DISCORD-JS-CRUD：提升 Discord 机器人开发体验
- Node.js v4.3.2版本Linux ARM64平台运行时环境发布
- SQLight：C++11编写的轻量级MySQL客户端
- 计算机专业毕业论文答辩PPT模板
- Wireshark网络抓包工具的使用与数据包解析
- Wild Match Map: JavaScript中实现通配符映射与事件绑定
- 毕业答辩利器：蝶恋花毕业设计PPT模板
- Node.js深度解析：高性能Web服务器与实时应用构建
- 掌握深度图技术：游戏开发中的绚丽应用案例
- Dart语言的HTTP扩展包功能详解
- MoonMaker: 投资组合加固神器，助力$GME投资者登月
- 计算机毕业设计答辩PPT模板下载
