非平衡系统中宏观长度相关性的实验意义与实现探讨

68 浏览量更新于2024-07-16 收藏 1.96MB PDF 举报

"非平衡系统中的宏观长度相关性及其可能的实现" 本文深入探讨了非平衡系统中的宏观长度相关性，特别是在能量密度或其他强度参数q经历有限变化率的情况下。作者Z.Nussinov指出，当系统从热力学平衡状态开始或结束，并在中间阶段经历这种变化时，相关性会呈现出独特的特性。特别是，研究发现，尽管在全局平均值q稳定后，站点间的一般关联函数Gij（即关联的协方差）的平均值可能趋向于零，但在长时间的平衡过程（如玻璃态物质中的情况）中，这种长距离的相关性可以持续存在。在玻璃态物质中，这种现象具有显著的意义。研究表明，理论预测的这种效应与过去十六年来的所有粘度测量结果一致，暗示了粘度的普遍崩溃。同时，作者还提到了非费米液体，这是另一个可能实现这些宏观长度相关性的领域。论文中进一步讨论了开放系统的有效平衡概念，通过不确定性关系建立不等式，将热容量与系统动力学联系起来。这些热不等式揭示，在温度为T的开放平衡系统中，最短的波动时间尺度通常与“普朗克”时间相关，即约为O(ħ/(kBT))。这里，ħ是约化普朗克常数，kB是玻尔兹曼常数，T是温度。此外，作者还短暂触及了量子测量、单一量子演化和热化过程之间的相似性，这为理解量子系统如何在非平衡状态下达到某种形式的统计平均提供了新的视角。这些研究不仅对理论物理学有重要意义，也为实验物理学家提供了一种可能的框架来检测和验证这些宏观长度相关性的存在。这篇研究为理解和探索非平衡系统的行为提供了新的洞察，特别是在长时间尺度下的动态和相关性。其结果可能对材料科学、量子信息处理以及更广泛的物理学领域产生深远的影响。

Z. Nussinov / Nuclear Physics B 953 (2020) 114948 15

state displaying (at all sites i) a uniform value of S

. Even though there are no connected corre-

lations of the energy densities themselves in the initial state, the non-local entanglement enables

long range correlations of the local energy densities once the system is evolved with a transverse

ﬁeld. The variance σ



should not, of course, be confused with the spread of energy densities that

the system assumes as it evolves (e.g., for the S

tot

=0 state, σ



=O(1) while the energy density

(t) does not vary with time). We nonetheless remark that the standard deviation σ



vanishes at

the discrete times t

=kπ/B

(with k an integer) – the very same times where the rate of change

of the energy density (t) is zero.

We now turn to the higher order moments of the ﬂuctuations of the t>0 states evolved

with Eq. (8), ()

 ≡

(H

spin

−H

spin

)

 with p > 2. (The standard deviation of

Eq. (9) corresponds to

p =2.) Here, H

spin

(t) = (T e





)dt



spin

T (e

−





)dt



) is the

Heisenberg picture Hamiltonian and the expectation value is taken in the initial state |ψ

Spin

.

If N  1 and 1 > |w| then S

tot

, S

tot

 =

√

tot

+1) −m(m ±1)|S

tot

, m ± 1 ∼

tot

√

1 −w

tot

, m ± 1 where S

tot

= m

h. Trivially, for all

m and m



, the matrix element

of δS

tot

≡ S

tot

−S

tot

 between any two eigenstates, S

tot

, m|δS

tot

, m



 = 0. Thus, the

only non-vanishing contributions to ()

 stem from (S

tot

)

. This expectation value may

be ﬁnite only for even

p. Thus, in what follows, we set p = 2g with g being a natural num-

ber. For S

tot

= O(N), when expressing the expectation value of ()

 longhand in terms

of spin raising and lowering operators, one notices that, in this large N limit, each individual

term containing an equal number of raising and lowering operators yields an identical contri-

bution (proportional to (S

tot

√

1 −w

)

) to the expectation value ()

. Since there are





such contributions, for all g  N in the thermodynamic (N →∞) limit, the expectation

value ()

 =





(



)

. We write the ﬁnal (Schrodinger picture) state at time t = t

|ψ

Spin

 =



|φ

. The probability distribution of the energy density of Eq. (2) reads

P(



) =



δ(



−

). (11)

In this example, the Heisenberg picture Hamiltonian H

spin

(and the associated operators H

)

remains local for all times. In general systems, the time evolved Heisenberg picture Hamil-

tonian need not be spatially local. Eq. (11) describes the probability distribution associated

with the “wave packet” intuitively discussed in Section 4 (a “packet” that is now given by

the amplitudes {c

} in our eigenvalue decomposition of the ﬁnal state |ψ

Spin

). The averaged

moments of 



≡ (



− ) are ()

 =



d



P(



)(



− )

. Here, as throughout,  =

ψ

Spin

spin

|ψ

Spin

 =−(



tot

cos θ(t

))/N is the energy density in the ﬁnal state

(i.e., the average of the energy density 



when weighted with P(



)). More generally, the expec-

tation value of a general function f(

spin

) in the state |ψ

Spin

(or, equivalently, of f(

spin

) in the

above deﬁned ﬁnal Schrodinger picture state |ψ

Spin

) is given by f(

spin

) =



d



f(



)P (



The mean value of each Fourier component e

iq(



)

when evaluated with P(



) is

e

iq(



)

=

∞



g=0

(iq)

(2g)!







∞



g=0

(−1)

(g!)

(

qσ



√

)

(qσ



√

2), (12)

where J

is a Bessel function. An inverse Fourier transformation then yields

16 Z. Nussinov / Nuclear Physics B 953 (2020) 114948

P(



) =

θ(σ



√

2 −|



πσ





2 −

(



)

(σ



)

. (13)

Here, as earlier, 



denotes the difference between 



and the value of the energy density (t).

The Heaviside function θ(z) in Eq. (13) captures the fact that the spectrum of H

spin

is bounded.

Similar results apply to boundary couplings [60]. The distribution of Eq. (13)may also be ratio-

nalized geometrically as we will shortly discuss (Eq. (16)). Comparing our result of Eq. (13)to

known cases, we remark that, where it is non-vanishing, the distribution of Eq. (13)is the recip-

rocal of the W

igner’s semi-circle law governing the eigenvalues of random Hamiltonians and the

associated distributions of Eq. (11), e.g., [61]. We stress that Eq. (13)is exact for the general spin

Hamiltonians of Eqs. (6), (8) and does not hinge on assumed eigenvalue distributions of effective

random matrices.

Performing additional calculations, we ﬁnd qualitati

vely similar results for analogous “cool-

ing/heating” protocols. For instance, one may consider, at intermediate times 0 ≤ t ≤ t

, the

Hamiltonian governing the system to be that of a time independent H

(i.e., one with a con-

stant B

(t) = B

) augmenting H

spin

instead of replacing it. That is, we may consider, at times

0 ≤t ≤t

, the total Hamiltonian to be

spin

. (14)

For such an augmented total Hamiltonian H

, the total spin



tot

precesses around direction of the

applied external ﬁeld (B

ˆe

) ≡B ˆe

. An elementary calculation analogous to that leading

to Eq. (9) then demonstrates that the corresponding standard deviation σ



of the energy density

at t = t



(t =t

) =

tot

√



1 +

tot

−w



sin

(Bt

) +

(1 −cos(Bt

))

. (15)

We wish to stress that if S

tot

= O(N ) and |w| < 1 then, as in Eq. (9), the standard deviation



= O(N) for general times t

. The distribution of the energy density following an evolution

with this augmented Hamiltonian will, once again, be given by Eq. (13)for macroscopic systems

of size N →∞. The reader can readily see how such spin model calculations may be extended

to many other exactly solvable cases. The central point that we wish to underscore is that a br

oad

distribution of the energy density, σ



=0, is obtained in all of these exactly solvable spin models

in general dimensions.

6.1.2. Semi-classical spin systems and a g

eometrical interpretation

The results that we just deri

ved are valid for any spin S realization of the Hamiltonians of

Eqs. (6), (8). The standard deviations of Eqs. (9), (15) remain ﬁnite for all S (with a scale set by

the external magnetic ﬁeld energies in these Hamiltonians). As long known [62,63], the S →∞

limit yields classical renditions of respecti

ve quantum spin models. Thus, the ﬁnite standard

deviation of the energy density in individual eigenstates (Eqs. (9), (15)) and in thermal states

formed by these eigenstates implies that the standard deviation of the energy density remains

ﬁnite in the classical limit (as wa

s suggested by the general arguments associated with Eq. (4)).

More strongly, all that mattered in our earlier calculation of Section 6.1.1 were the S

tot

and

Z. Nussinov / Nuclear Physics B 953 (2020) 114948 17

Fig. 4. (Color online.) Semi-classically, the total spin



tot

may, with equal probability, correspond to any vector connect-

ing

the origin of a sphere of radius

tot

to a point along a ring forming “a line of latitude”. In the ﬁgure above, this

“line of latitude” ring is deﬁned by boundary of the shaded spherical cap near the “north pole”. All points along the line

of latitude share the same value of S

tot

. Here, in the initial state, the polar angle θ =0.

Fig. 5. (Color online.) Applying the transverse ﬁeld of Eq. (8)to the ring of Fig. 4 leads to precession about the S

tot

axis.

For the above displayed ring, θ(t) = π/2. During the precession, the semi-classical total spin vectors



tot

on the ring

acquire a range of possible S

tot

values leading to the standard deviation σ



of the energy density of Eq. (6). The simple

(semi-classical) calculation of Eq. (16)for the distribution of S

tot

values for such a uniform ring leads anew to Eq. (13).

tot

values. If S

tot

= O(N ) then even if the size of the spin S at each lattice site is small, the

total system spin



tot

is a macroscopic classical quantity and our results may be reproduced

by a computation for semi-classical spins. Indeed, an explicit calculation for classical spin states

trivially illustrates that a ﬁnite standard deviation σ



> 0may arise in semi-classical systems [64].

To make this explicit, we now perform such a computation. This rather elementary calculation

will link the geometry of the manifold of possible S

tot

values to the full distribution P(



) of the

possible energy densities. Towards this end, we parameterize the semi-classical total spin by a

vector



tot

on a sphere of ﬁxed radius S

tot

(the application of the transverse ﬁeld Hamiltonian of

Eq. (8) does not alter (



tot

)

). Herein, at any time t, the vector



tot

may correspond, with equal

probability, to any vector on a circular ring, see, e.g., Figs. 4 and 5.

In Eq. (13), 



denotes the difference between 



and the average energy density (t). At

time t, along a ring (see, e.g., Fig. 5), that is further parameterized by an azimuthal angle ϕ



the possible values of S

are given by S

tot

(ϕ



, t) =S

tot

(t) +S

tot

√

1 −w

sin θ(t) cos ϕ



. Here,

18 Z. Nussinov / Nuclear Physics B 953 (2020) 114948

θ(t) becomes the polar angle of the center of mass of the ring (i.e., θ(t) is the angle between

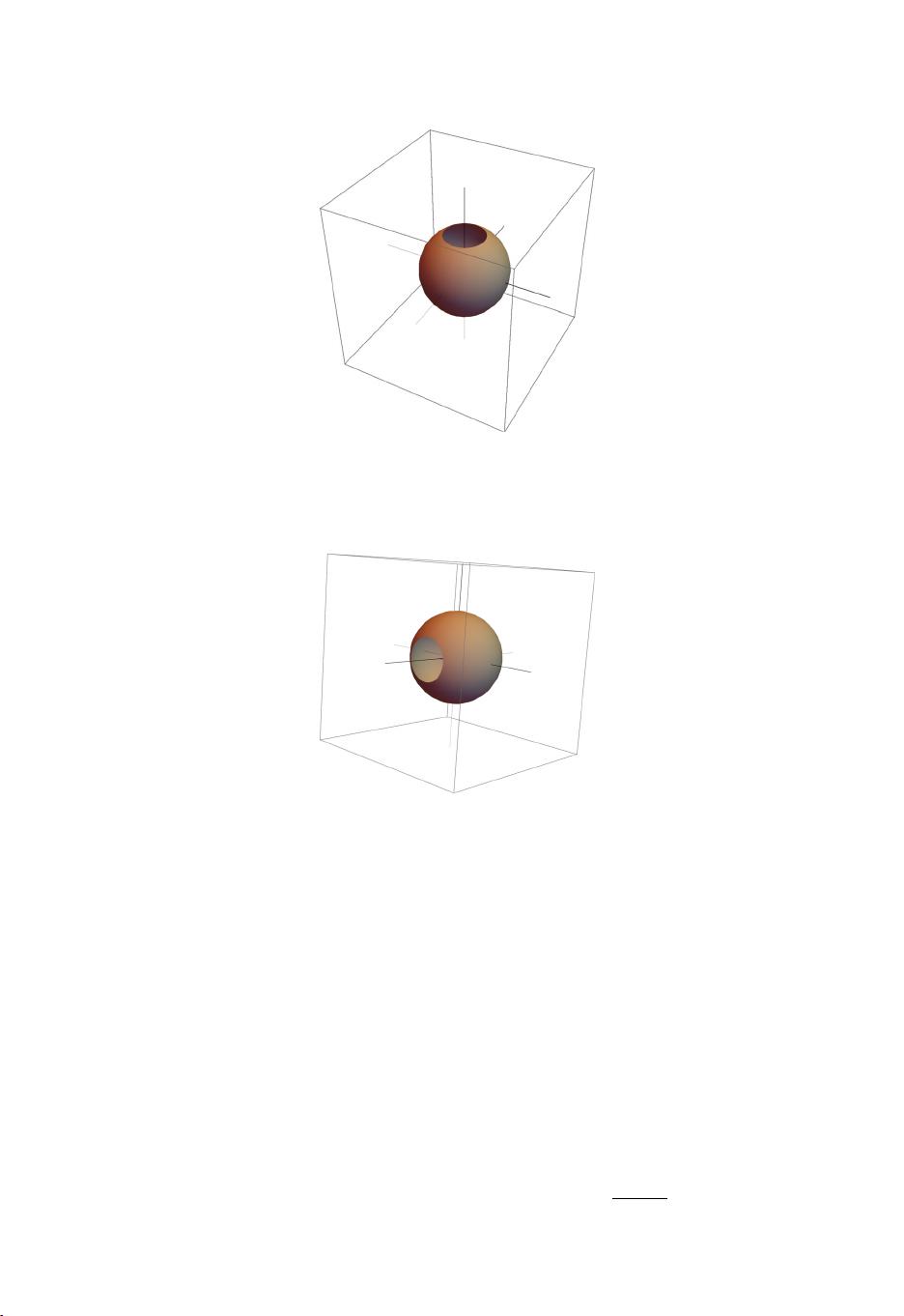
(i) a vector connecting the origin to the center of the center of the ring (see, e.g., Figs. 4 and

5) and (ii) a vector along the positive S

tot

axis). The expectation value S

tot

 is that of S

tot

the time evolved state (classically, it is the average of S

tot

around the full ring (0 ≤ ϕ



< 2π)

at time t), i.e., S

tot

(t) = S

tot

cos θ(t). The possible values of S

(ϕ



) appear symmetrically twice

in the interval 0 ≤ ϕ



< 2π. We may thus consider only 0 ≤ ϕ



<π. By the normalization of

the probability distribution for ϕ



and the corresponding probability distribution for the energy

density, P(



)d



dϕ



. Thus,

P(



) =



dϕ



d





∂S

tot

(ϕ



)

∂ϕ





. (16)

Combining Eq. (9)(which may derived from a geometric analysis of Fig. 5 as we next ex-

plain) with Eq. (16) then provides Eq. (13). We may indeed readily calculate the spread σ

tot

of S

tot

values and rationalize the ﬁnite standard deviation σ



of Eq. (9) from simple geo-

metric considerations, when 1/S

tot

is set to zero (the semi-classical limit). From geometry,

tot

ring

√

| sin θ(t)| ≡R

| sin θ(t)| where R

ring

= S

tot

√

1 −w

. Here, R

is the radius of gy-

ration of the ring of Fig. 5 (corresponding to θ = π/2) about an axis parallel to the S

tot

axis that

passes through the center of mass of this ring. The ﬁnite radius of gyration R

= 0 implies a

spread of energy densities σ



sin θ(t)|R

= 0at general times. This semi-classical result for



coincides with Eq. (9). We will further comment on the |w| = 1 states below and at the end

of Section 6.1.3. We now ﬁrst brieﬂy comment on another trivial limiting case. When w =0, the

initial state will correspond, in the description of Fig. 4, to the equator. Applying a transverse

ﬁeld will then lead to a rotation of the equator around the S

tot

axis; this so generated ring (an-

other great circle on the sphere) will, generally, display a non-vanishing spread of S

tot

/N values

(leading to σ



=0). However, when the initial state has w = 0, such a rotation will not yield any

change in the energy density, d/dt = 0. This trivial limiting case illustrates that, as a matter of

principle, a ﬁnite rate of variation of the energy density is not mandatory in order to a ﬁnite ha



. As we demonstrate in the current work, the converse statement holds (a ﬁnite d/dt implies

a ﬁnite σ



Although the Hamiltonian of Eq. (6)is extremely general as are its eigenstates of high to-

tal spin S

tot

= O(N ) (e.g., states of large total spin in typical low temperature ferromagnets),

characteristic equilibrium states of this Hamiltonian will correspond to a special subset having

|w| = 1 (that is, the total spin will be polarized along the externally applied ﬁeld direction). As

we discussed earlier, such equilibrium states will thus emulate product states (in which all indi-

vidual spins assume the same polarization). Thus, as wa

s indeed evident in Eqs. (9), (15), when

w =±1, the broadening σ



=0. In a related vein, the fully polarized state – a coherent spin state

on a sphere of radius S

tot

– is rotated “en block” without any other change of the wavefunction

under the action of a transverse ﬁeld. To see the effect for our exactly solvable system, we have

to go away from the limit |w| = 1. Away from this limit, the state of the system evolves non-

trivially. In the parlance of Section 4, when e

volving under the transverse ﬁeld Hamiltonian of

Eq. (8), the |w| =1spin state is not merely “translated” (rotated on a sphere of radius S

tot

) with

no other accompanying changes. Appendix J discusses a gedanken experiment in which starting

from an equilibrium state, one may apply transverse ﬁelds and let the closed system equilibrate

anew so as to generate a state |ψ

Spin

 of total spin S

tot

=O(N) with w =±1.

Z. Nussinov / Nuclear Physics B 953 (2020) 114948 19

6.1.3. Causality, correlations, and a ﬁnite

d

We now return to the qualitative discussion of Section 4 concerning the causal generation

of long range correlations in real physical systems. Eq. (4) suggests that long-range correla-

tions emerge from the coupling between an external environment (which we have not explicitly

included in the model system in this Section) to the system bulk (e.g., the global coupling of

Eq.

(8)). As we will demonstrate in Appendix B, compounding the lack of causal correlations

in relativistic systems, when the environment is included also in non-relativistic systems obey-

ing Lieb-Robinson type bounds [8–11,30], a ﬁnite rate of variation of the energy density cannot

appear at short times t<

min

= O(L/v

). Thus, generally, effective global couplings such as

those of Eq. (8) cannot appear instantaneously. We wish to reiterate this particular point. Without

the bulk coupling of Eq. (8) (and ensuing correlations), the system cannot exhibit a ﬁnite rate

of change of its energy density (i.e., without such a global coupling, the latter rate of change

d

=0). It is only after long enough times (such as those implied by the Lieb-Robinson bounds

of Appendix B), at t>t

min

, that a global coupling such as that of Eq. (8)may appear in effec-

tive descriptions not explicitly involving an external environment. Only at these sufﬁciently long

times, our obtained results for the correlations hold.

We note anew that in an equilibrium state of the Hamiltonian of Eq. (6), the total spin will

be polarized along the applied ﬁeld direction and w = 1. In such a case, for the realization

of various gedanken experiments (e.g., Appendix J), long-range correlations (Appendix I) may

indeed appear in the system after a time that scales with the system size.

As noted after Eq.

(9), the calculation of the energy density and its standard deviation for a

|w| =1system evolving under Eq. (8)is identically the same as that for a product state of S

tot

spins. In the representation of Section 6.1.2 , such an initial ferromagnetic state will correspond

to a single point on the sphere (the north or south pole) instead of the ring in Fig. 4; a rotation by

a transverse ﬁeld as depicted in Fig. 5 will then lead to this point rotated elsewhere – there will

not an

y spread of the S

tot

values and σ



=0. That such a ferromagnetic state (akin to the product

states discussed earlier) exhibits no spread of the energy density is consistent with Section 5.

Further, in tandem with our main thesis concerning a typical general trend between the energy

changes and long range correlations, for w = ±0, 1 states, at those times at which the ener

density changes at a vanishing rate d/dt =0 (corresponding to θ(t) ≡0(

mod π)), the standard

deviations of the energy density (and the associated long-range correlations that it implies) also

vanishes, σ



=0.

6.2. Itinerant hard core Bose systems

Our spin model of Section 6.1 can be deﬁned for local spins of any size S. The function P(



)

of Eq. (13) characterizing our investigated states is not a very typical probability distribution.

However, the non-local entangled character of states having a ﬁnite energy density relative to

the ground state is pervasive for thermal states. This model can be recast in different ways.

In what follows we focus on the spin S = 1/2

realization of Eq. (6). The Matsubara-Matsuda

transformation [65,66] maps the algebra of spin S = 1/2 operators onto that of hard core bosons.

Such hard core bosons may, e.g., emulate Cooper pairs in superconductors in the limit of short

coherence length. Speciﬁcally, the hard core bosonic number operator at site i is n

= b

†

0, 1 with b

and b

†

the annihilation and creation operators of hard core bosons ((b

†

)

= b

0, [b

, b

†

] = (1 − 2n

)δ

). Following this transformation, the spin Hamiltonian of Eq. (6)is

converted into its hard core bosonic dual,

剩余90页未读，继续阅读

weixin_38695061

粉丝: 4
资源: 931

非平衡系统中宏观长度相关性的实验意义与实现探讨

网络游戏-社交网络系统中的认知相关性定位.zip

论文研究-我国沪深300股指期货和现货市场的交叉相关性及其风险.pdf

MATLAB控制策略优化：动态系统仿真的实现与性能提升

AI在教育中的新篇章：个性化学习路径设计的五大创新策略

【金融数据新视角】：RNN在金融分析中的应用，时间序列预测与风险管理

C#ASP.NET网络进销存管理系统源码数据库 SQL2008源码类型 WebForm

(源码)基于ZooKeeper的分布式服务管理系统.zip

23python3项目.zip

技术资料分享AL422B很好的技术资料.zip

c语言俄罗斯方块.rar

最新资源