图数据结构详解：遍历、最短路径与拓扑排序

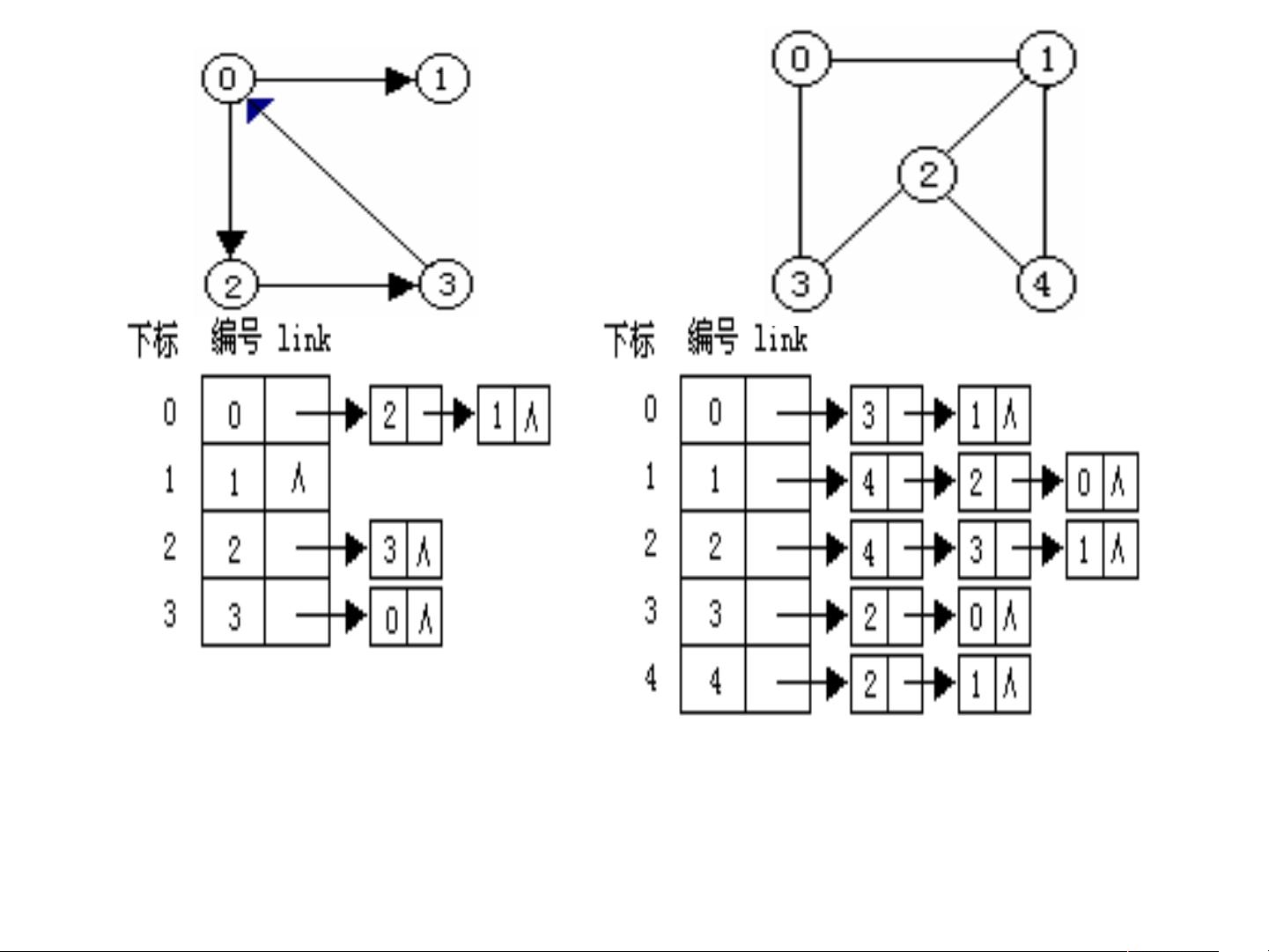
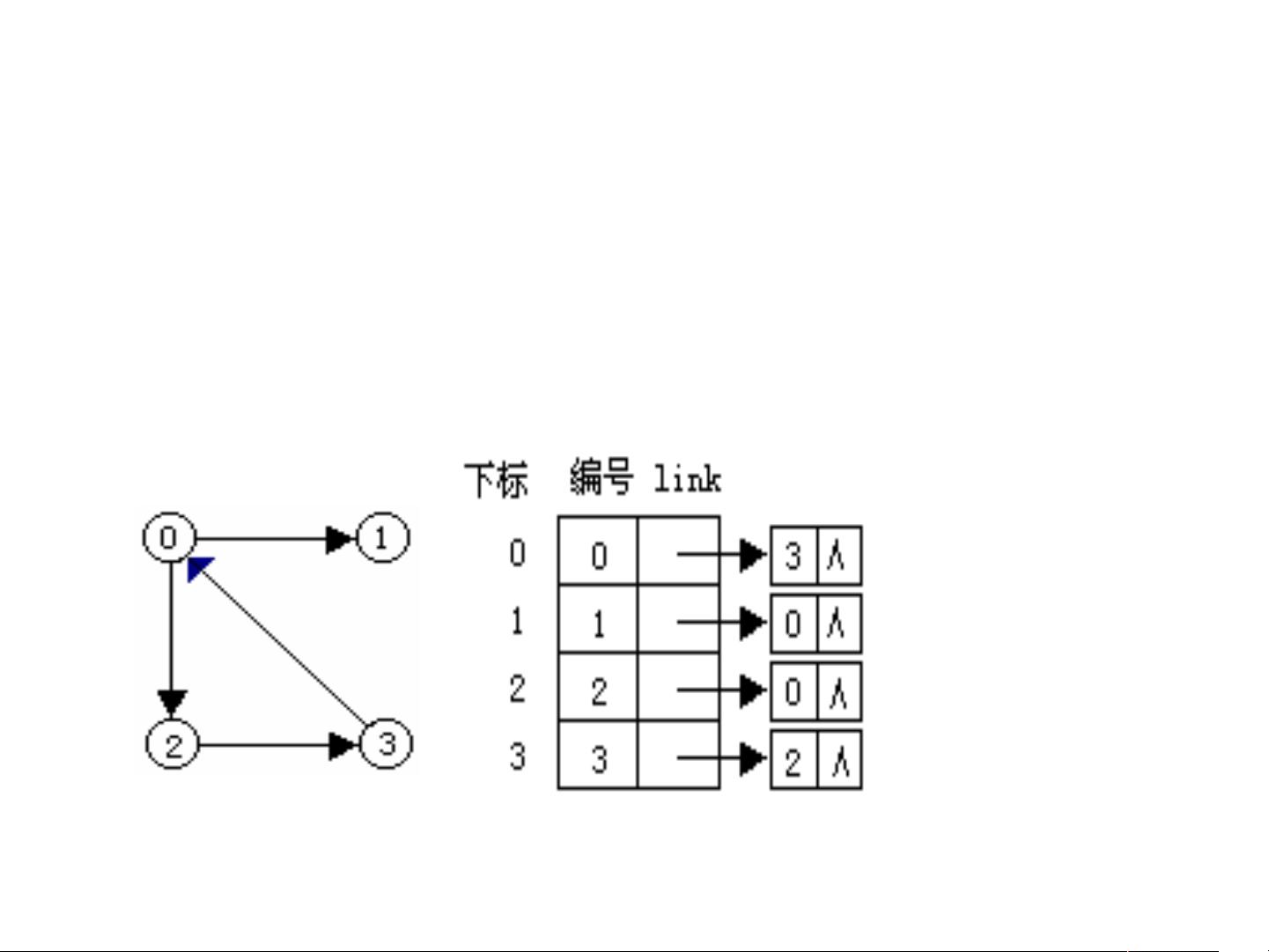
"数据结构第七章图.ppt" 在数据结构中，图是一种非常重要的非线性数据结构，它的概念和应用广泛。图由顶点（数据元素）和边（顶点之间的关系）组成，可以表示各种复杂的关系，如城市间道路、社交网络联系等。图分为有向图和无向图，有向图的边具有方向性，而无向图的边没有方向。图的存储结构通常有邻接矩阵和邻接表两种方式。 1. **图的定义和术语**： - 图（Graph）由顶点集V和边集E组成，记作G=(V,E)。 - 顶点（Vertex）是数据元素，边（Edge）是顶点之间的关系。 - 有向图的边是有序的，称为弧，如<u,v>表示从u到v的弧。 - 无向图的边是无方向的，如(u,v)。 - 度（Degree）：无向图中，顶点的度是其关联边的数量；在有向图中，入度是进入顶点的边数，出度是离开顶点的边数，总度是入度加出度。 - 子图（Subgraph）是原图的一部分，包含在原图的顶点和边中。 2. **图的存储结构**： - 邻接矩阵（Adjacency Matrix）：使用二维数组存储图，数组的每个元素代表一对顶点之间是否有边相连。 - 邻接表（Adjacency List）：为每个顶点维护一个链表，链表中包含所有与其相邻的顶点。 3. **图的遍历**： - 深度优先遍历（Depth-First Search, DFS）：从某个顶点出发，尽可能深地探索图的分支，直到访问所有可达顶点。 - 广度优先遍历（Breadth-First Search, BFS）：从源点开始，逐层访问所有邻居，然后访问下一层的顶点。 4. **生成树**： - 一棵生成树是图的一个子集，包含了图的所有顶点，并且边构成了一棵树的结构，没有环路。 5. **最短路径**： - Dijkstra算法：用于寻找单源最短路径，适用于带非负权重的图。 - Bellman-Ford算法：处理可能有负权重边的情况，也能找到最短路径。 6. **拓扑排序**： - 对于有向无环图（DAG），拓扑排序是将顶点排成线性序列，使得对于每条有向边(u,v)，u都在v之前。 这些概念和算法在解决实际问题时非常有用，如网络路由、任务调度、社会网络分析等。理解并掌握图的理论和实现方法对于计算机科学的学习和实践至关重要。