the gray values of P equally spaced pixels on a circle of radius
R(R4 0) that form a circularly symmetric neighbor set. And
sðxÞ¼
0,xZ 0
1,xo 0
(
. Finally, according to the rule utilized in Ref.
[17], a binary factor 2
p
is assigned to each neighbor. The original
LBP value of a pixel is represented by
LBP ¼
X
P1
p ¼ 0
ðsðg
p
g
c
Þ2
p
Þð2Þ
The LBP descriptor labels the pixels of an image by determin-
ing the gray levels of the P neighbors (with radius R) of the center
pixel as shown in Fig. 3. Finally, the histogram of the labels is
utilized for texture description.
Ojala et al. [18] extend the original LBP descriptor to multi-
resolution LBP by using neighbors of different sizes. Using circular
neighborhoods and interpolating the pixel values allow any
radius and number of pixels in the neighborhood as shown in
Fig. 3. Thus the final multi-resolution LBP (denoted MLBP)is
constructed as follows:
MLBP ¼[
P,R
LBP
P,R
¼/LBP
P
1
,R
1
;...;LBP
P
S
,R
S
S ð3Þ
where P
i
and R
i
(i¼1,y,S) denote the neighbor number and
radius. The combination can improve the discriminative power
of the texture descriptors. However MLBP descriptors are
obtained from the same image with fixed resolution. MLBP
represents multi-resolution texture information by sparse sam-
pling [29]. Maenpaa et al. [28,29] have pointed out that this
representation approach is sensitive to noise, because sampling is
made at a single pixel position rather than an effective region.
Moreover, direct sampling usually causes aliasing effects [28,29].
To overcome the above two shortcomings, multi-resolution LBP
descriptor are proposed by utilizing low-pass filtering (LBPF) and
local averaging [28–30]. In LBPF, each sample in the neighborhood
can be made to collect intensity information from a large effective
area rather than a single pixel as shown in Fig. 6. The relationship
of LBPF and the proposed PLBP is deeply analyzed in Section 2.3.
Local Gabor binary pattern is extracted by carrying out Gabor
transform for the image with n-scale and m-orientation filtering
[21]. This method improves the discriminative power of original
LBP [17]. In this paper, we also represent LGBP in spatial pyramid
domain. Experimental results are given in Section 4.2.
2.2. Local binary pattern represented in spatial pyramid domain
Pyramid transform is an effective multi-resolution analysis
approach. In this paper, we represent local binary pattern in
spatial pyramid domain.
During pyramid transform, each pixel in the low spatial
pyramid is obtained by down sampling from its adjacent low-
pass filtered high resolution image as shown in Fig. 4(b). Thus in
the low-resolution images, a pixel corresponds to a region in its
high-resolutions. In Refs. [28,29], Maenpaa et al. call the region as
‘‘effective area’’. Sequential pyramid images are constructed as
shown in Fig. 5. Each neighboring two images are with resolution
variation rate 2. That is to say, the down sampling ratios in x- and
y-directions are both
ffiffiffi
2
p
. Pyramid image can be generated by low-
pass filters of wavelet transform, Gaussian smooth filtering
[28,29], symmetric weighting and block averaging [30].
The pyramid generation approach consists of low-pass filtering
and down sampling images of the preceding pyramid level. Let f(x, y)
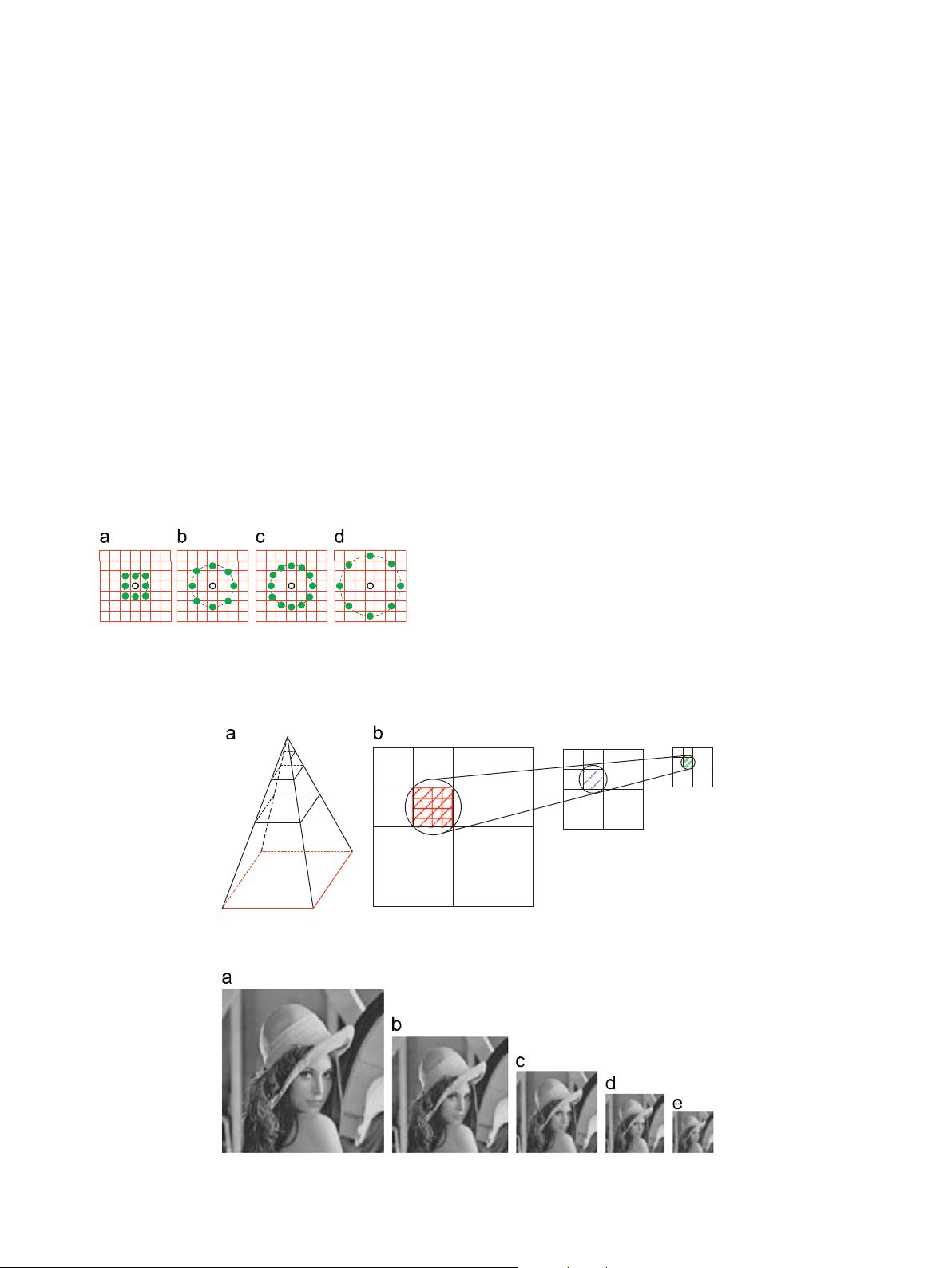
(8,2)(8,1) (12,2) (8,3)
Fig. 3. Four Examples of the LBP. (a) the circular (8,1) with P¼8 and R ¼1; (b) the
circular (8,2) with P¼8 and R¼2; (c) the circular (12,2) with P¼12 and R¼2; and
(d) the circular (8,3) with P ¼8 and R ¼3. The pixel values are interpolated
whenever the sampling point is not in the center of a pixel.
Level 1
Level 2
Level 3
Level 4
Fig. 4. Diagram of pyramid transform and spatial pyramid sampling. (a) A four level spatial pyramids are shown. (b) The diagram of pyramid sampling in neighboring
3 resolutions. The down sampling ratios in x- and y- directions are both 2. The resolution variation of neighboring two pyramids is with a factor 4.
Fig. 5. Gaussian Pyramid images. The original image (level 1) and their Gaussian pyramids shown from left to right. The resolution variation of two neighboring pyramid is
2, that is to say the down sampling ratio is with a factor
ffiffiffi
2
p
in both x- and y- directions.
X. Qian et al. / Pattern Recognition 44 (2011) 2502–25152504









