二叉树详解：概念、形态与特性

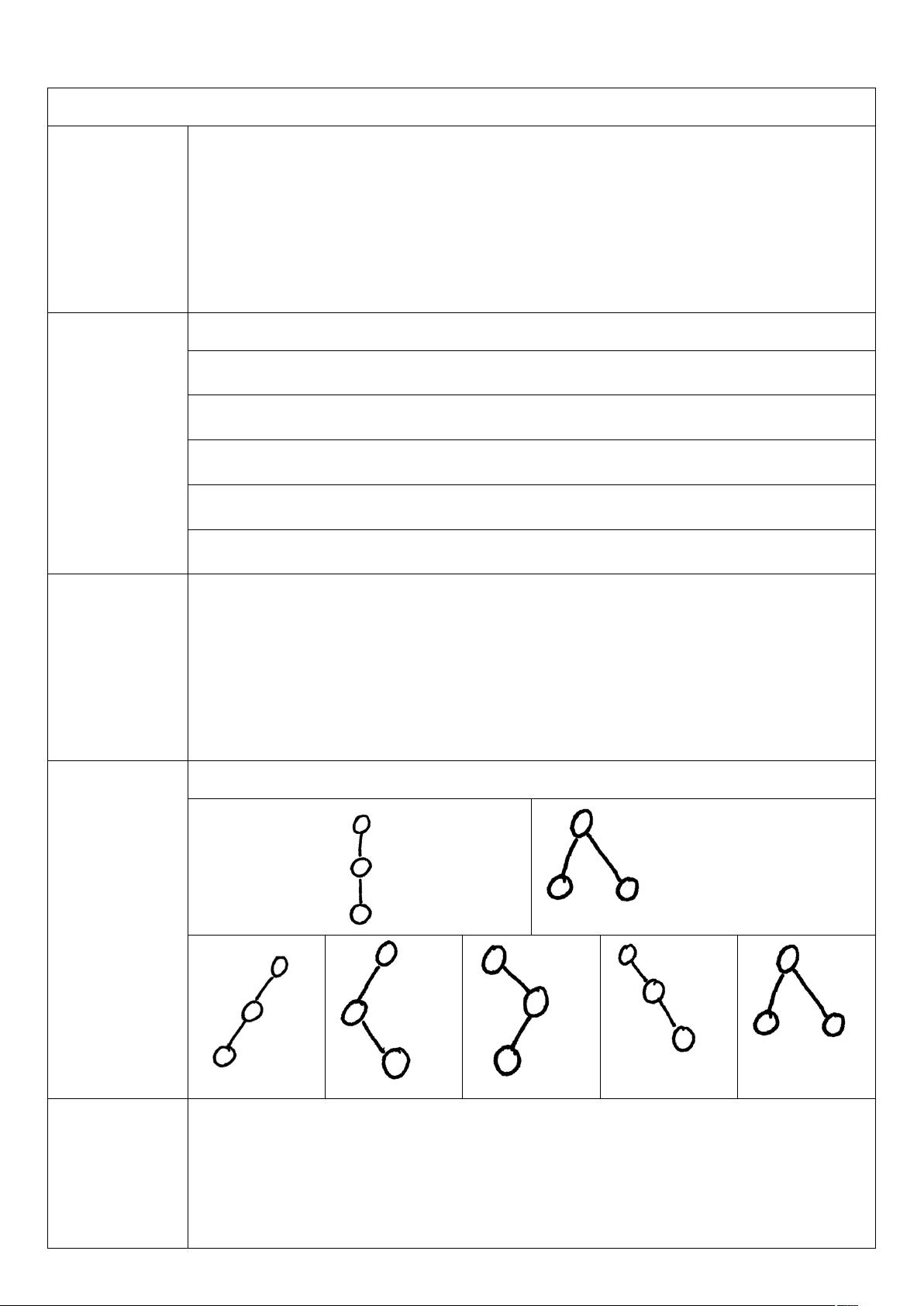
"二叉树相关的五个重要知识点" 在数据结构中，二叉树是一种特殊的数据结构，它由n（n>=0）个节点组成，其中n=0表示空二叉树，n>0则表示非空二叉树，每个节点最多有两个子节点，即左子树和右子树。这种结构具有以下特点： 1. **二叉树的形态**： - **空二叉树**：没有任何节点。 - **单节点二叉树**：只有一个根节点。 - **左子树二叉树**：所有节点只有左子节点。 - **右子树二叉树**：所有节点只有右子节点。 - **双子树二叉树**：既有左子树也有右子树。 2. **二叉树的特性**： - **度限制**：每个节点最多有两个子节点，不存在度大于2的节点。 - **子树顺序**：若节点只有一个子树，必须指定它是左子树还是右子树。 3. **三个节点的树与二叉树形态**： - 三个节点可以构成五种不同的树形，包括三种二叉树形态（一个根节点，一个左子节点，一个右子节点），以及两种非二叉树形态（一个根节点，两个左子节点或两个右子节点）。 4. **单支树**： - **左单支树**：所有节点只有左子节点，特点是各层只有一个节点，节点个数等于其深度。 - **右单支树**：所有节点只有右子节点，同样具备上述特点。 - **斜树**：左单支树和右单支树的总称，它们在同样高度的二叉树中结点数最少，高度相同的情况下结点数最多。 5. **满二叉树与完全二叉树**： - **满二叉树**：所有分支节点都有左右子树，叶子节点都在最底层。特征包括：叶子节点只能在最下层，只有度为0和2的节点，满二叉树的节点数最多，叶子和分支节点数也最多。 - **完全二叉树**：对于n个节点的二叉树，如果与满二叉树的节点排列一致，则是完全二叉树。满二叉树是完全二叉树的一种特殊情况，完全二叉树的深度为k时，k-1层是满的。叶子节点出现在最下层，最下一层的叶子节点集中在左侧。 这些知识点是理解、操作和应用二叉树的基础，它们在算法设计、数据存储和搜索等领域有广泛应用，如二叉搜索树、堆排序、哈夫曼编码等。掌握二叉树的性质和操作，能帮助我们更好地解决复杂问题，提高编程效率。