神经网络基础：线性与非线性激活函数解析

"高级人工智能-神经网络.ppt" 在高级人工智能的领域中，神经网络是研究和应用的重要组成部分。本资料详细介绍了神经网络的基础概念，包括神经元模型、基本函数和激活函数。共有138页的内容，深入探讨了神经网络的理论与实践。 神经网络的构建基于神经元模型，如图3.1所示，它由多个输入分量x1到xm和一个输出分量yj组成，每个输入分量通过相应的权重wj连接到神经元。权重w0通常代表阈值，而wij表示输入xi与神经元输出之间的关系。这种结构允许神经元对不同输入的加权组合进行响应。 基础函数（Basis Functions）是神经网络计算的核心元素。常见的基础函数有： 1. 线性基本函数（Linear Basis Functions）：其输出是输入向量x与权重向量w的线性组合。线性函数在输入空间中定义了一个超平面，可以看作是输入向量到阈值超平面的距离。 2. 径基函数（Radial Basis Functions, RBFs）：以输入向量x与中心向量μ之间的欧几里得距离为基础，常用于聚类和插值。RBFs在输入空间中定义了一个以中心μ为中心，半径为r的超球体。 3. 椭圆基本函数（Ellipse Basis Functions, EBFs）：这是RBFs的一种推广，考虑了输入空间的非均匀扩展。EBFs通过不同的半轴长度aμi定义了一个超椭球体，可以适应数据的多维度分布。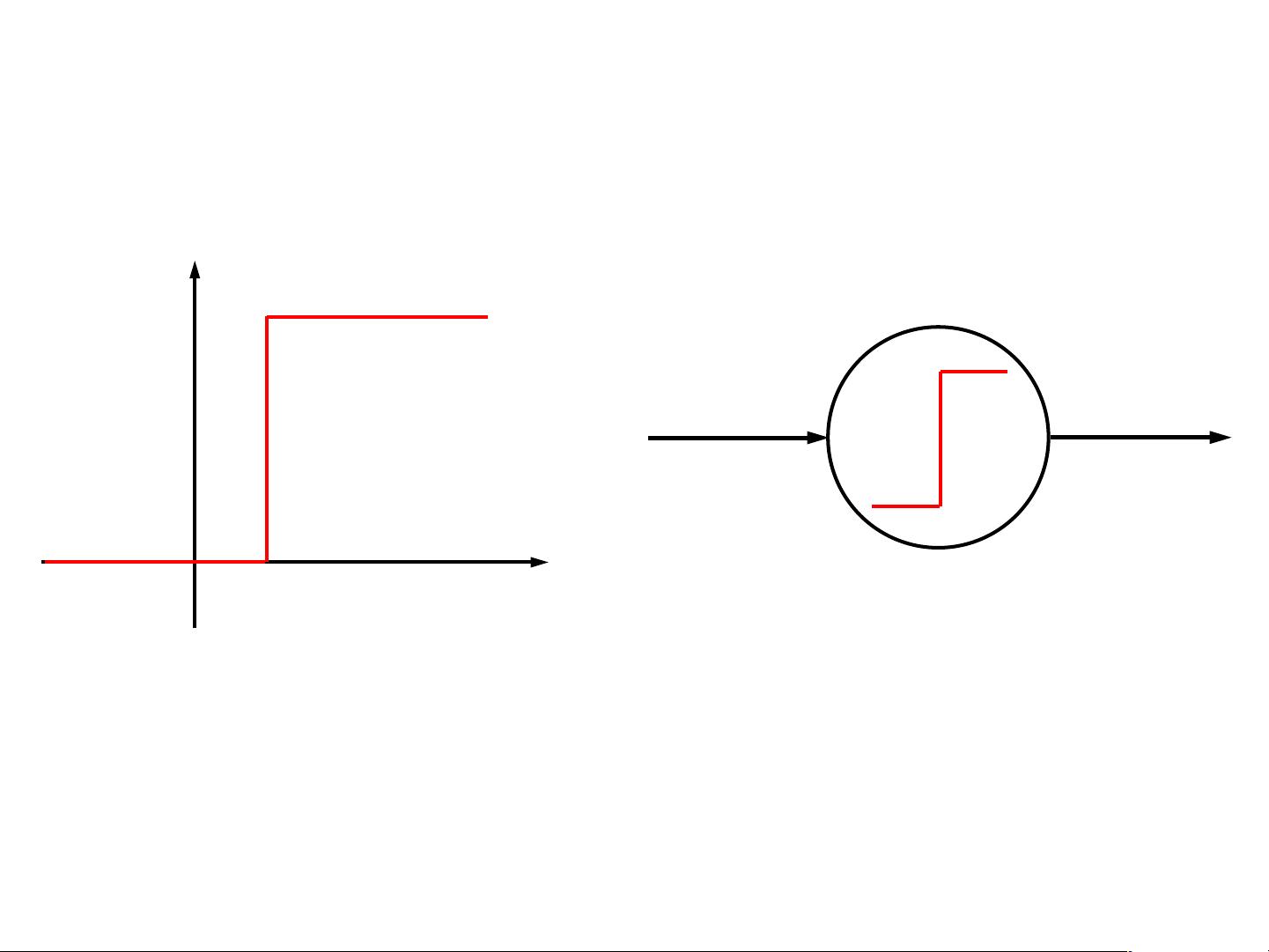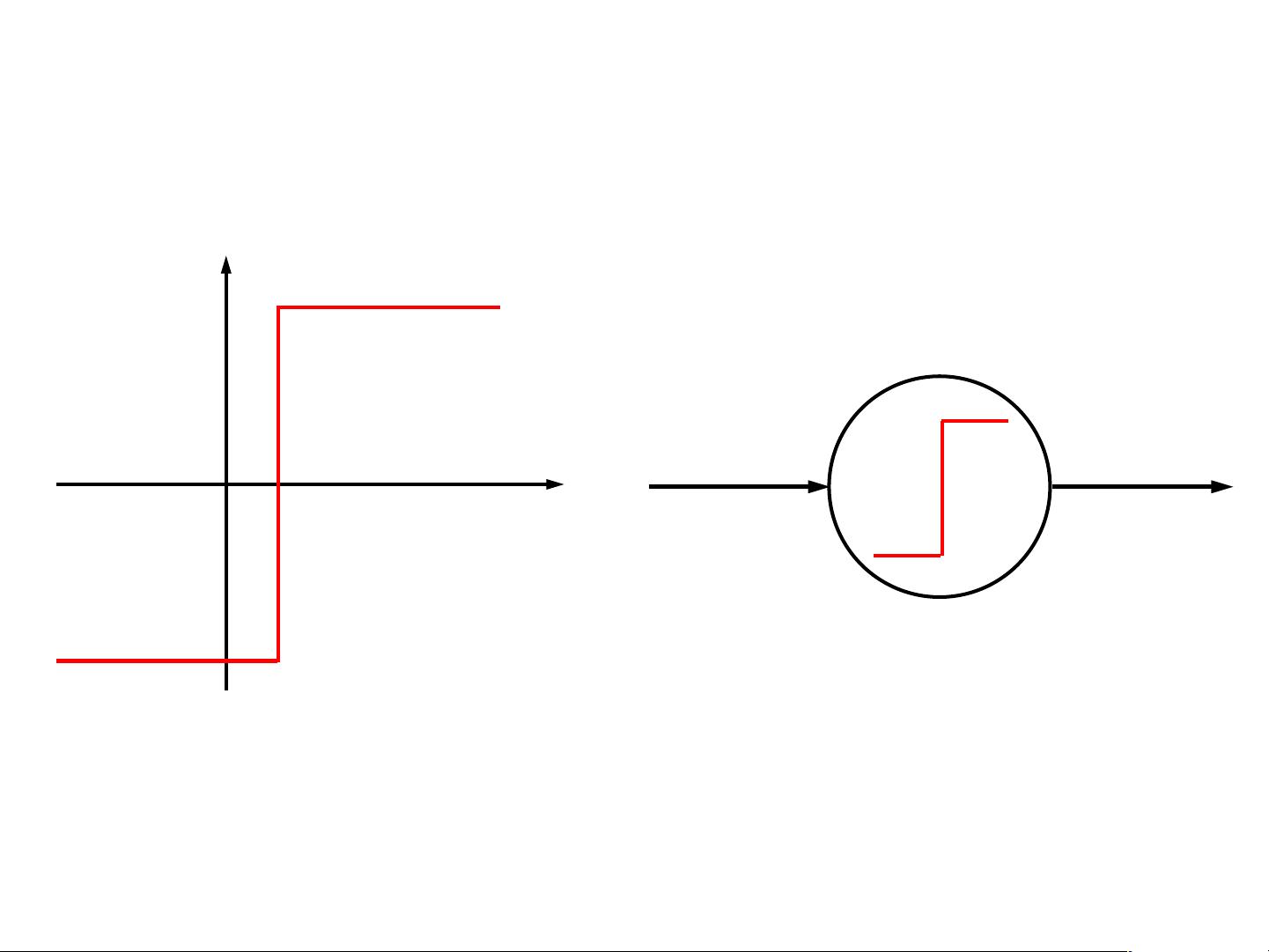 激活函数（Activation Functions）是神经元的实际输出y与总输入z之间的非线性转换，使得神经网络能够处理复杂的非线性问题。典型的激活函数包括： - 线性激活函数：保持输入的线性关系，如线性函数y=z，通常用于输出层以保持连续性。 - 非线性激活函数：例如Sigmoid函数，将输入压缩到(0,1)之间，产生“阶跃”效果，适合二分类问题；还有ReLU（Rectified Linear Unit）函数，它在正区间内保持线性，在负区间设为0，有助于避免梯度消失问题。 此外，神经网络的学习过程涉及到权重的调整，这通常通过反向传播算法实现，它利用梯度下降优化损失函数，以最小化预测输出与真实输出之间的差异。神经网络的层数、神经元数量以及激活函数的选择都会影响网络的表达能力和训练效果。 神经网络是高级人工智能中的关键技术，通过模拟人脑神经元的工作原理，解决复杂问题，如图像识别、自然语言处理等。理解并熟练掌握神经网络的基本概念和运作机制，对于从事AI领域的研究和开发至关重要。